飞直，达米特（2019）

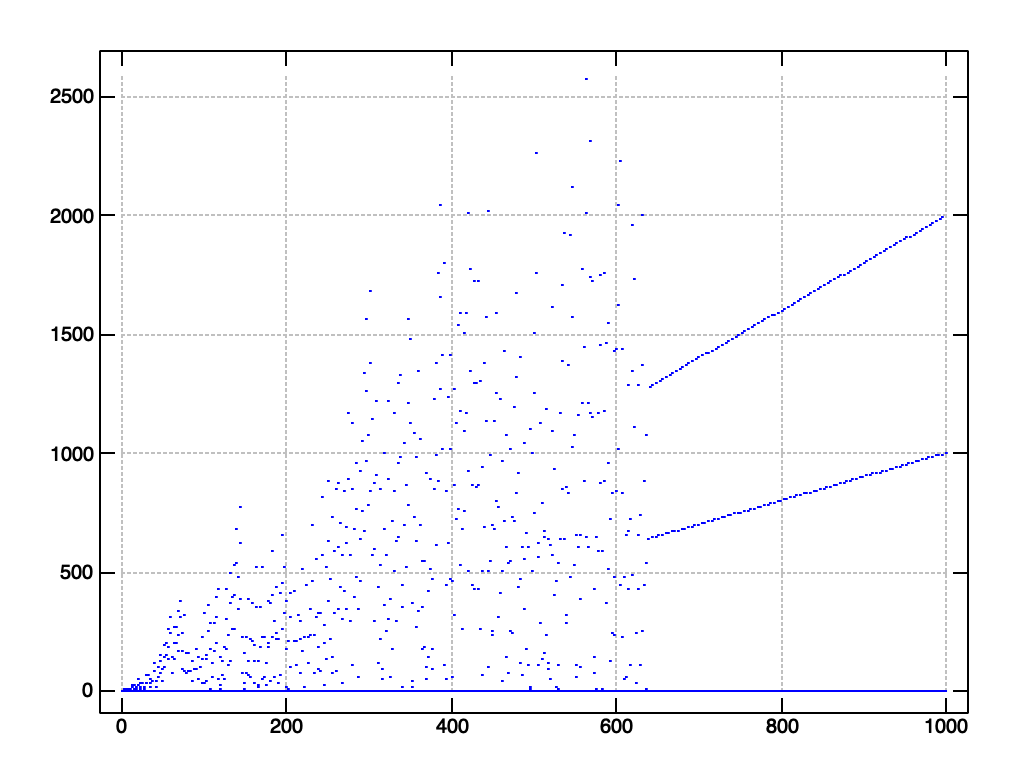
Tmallphile最近发布了一个关于一个有趣的递归函数的视频，称为“飞直，dammit！”当绘制时，最初似乎混乱，但经过六十三万八次迭代，瞬间稳定。

这听起来像是一个完美的弯曲我们的肌肉，并可统治自己的机会！

绘制我们的“飞直，达米特”的最简单方法使用J编程语言的图表是迫切方法：

A =：Monad定义if。 y＆lt; 2做。 1别的。 py =。 y - 1 gcd =。 y +。 py，如果。 1 = GCD。 1 + y + py其他。 py％gcd结束。结尾。）

我们已经定义了一个Monadic动词，如果我们通过“基本情况”值为0或1.否则，我们递归地在Y-1上执行A-1以获取我们的PY，或“前一个Y”。接下来，我们检查y和py的gcd等于1.如果它，我们返回1 + y + py。否则，我们将Py归还PY由GCD除以。

这是有效的，但它很慢。我们知道我们的递归调用正在做很多重复的工作。如果我们可以将我们的呼叫结果归功于A的结果，我们可以节省相当长的时间。值得庆幸的是，在J中的动词MEMOIZION与ADD M.添加到动词的声明一样简单：

虽然我们的初始解决方案工作并快速，但它并不利用什么使J成为独特而有趣的语言。让我们试着改变这个。

我们解决方案的肉是在两种情况下计算值。在y和py具有等于1的最大常见除数的情况下，我们计算1加y plus py。我们的势在必行，离开此计算的权利，如下所示：

我们也可以将其写成一个基本上读为“1加上X Plus Y的结果的”Monadic Noun Fork“：

同样，当我们遇到Y和Py之间最大的常见除数大于1时，我们想计算PY除以该GCD。这可以写成“二元叉”：

我们可以将此叉子读为“X除以X和Y最大的常见除容”。

既然我们将两种计算写为默认动词，我们可以使用“议程”动词（@。）来决定基于当前情况使用哪一个：

a_a =：1 + + a_b =：[％+ .a =：monad定义m.如果。 y＆lt; 2做。 1别的。 py =。 y - 1 has_gcd =。 1 = y +。 py py（a_b` a_a @。has_gcd）y结束。）

如果has_gcd为0，或“false”，我们将返回py a_b y的结果。否则，如果has_gcd为1，我们将返回py a_a y的结果。

我们可以详细说明使用议程来有条件地选择要申请的动词来帮助简化基本案例检查。

我发现自己从书籍和文章中产生了许多范围的内容，就像你＆＃39;现在重新阅读，以开源软件项目。如果你喜欢我的＆＃39; m做什么，没有什么能告诉你的支持，而不是注册我的邮件列表。

首先，让我们将我们的基本情况和递归案例定义为我们可以将其组合成GERUND的动词。我们的基础案例很简单。我们只想返回1：

recursive_case =：Monad定义M. py =。 y - 1 has_gcd =。 1 = y +。 py py（a_b` a_a @。has_gcd）y）

我们的函数，一个想要有条件地应用base_case或reachosive_case，具体取决于y是否大于或小于一个。我们可以编写使用议程：

而且我们的base_case动词很简单，我们只能彻底填写它清洁件：

a_a =：1 + + a_b =：[％+ .recursive_case =：monad定义m. py =。 y - 1 has_gcd =。 1 = y +。 py py（a_b` a_a @。has_gcd）y）a =：1：`reacursive_case @。 （1＆amp;＆lt;）

使用议程来构建条件和伪“案例语句”可以是将条件与J程序合并的强大工具。 它可以想到，您可能希望实现rocuRSive_case的默认版本。 不幸的是，我的J-FU不够强大，无法解决这个问题并提出一个理智的解决方案。 也就是说，Raul Miller用一线解决方案（在他的手机上）并在Twitter上发布了它。 劳尔的J-FU很强大。