数学家的尿布

自上次CP4SPACE文章的三个月主要花了解了一个名为Urbit的有趣项目。在Riva-Melissa Tez（以前的英特尔）在谈话中，我的注意力被吸引到它的存在性上继续改善硬件计算效率的重要性。

在互联网上写了一个体面的金额关于URBit，但它往往是非技术性的，解释项目的重要性，或者在高度非传统的项目特定的行话中编写的技术。相反，我们将通过审查数学家和理论计算机科学家最有可能感兴趣的Urbit的新颖内容来离开这些中的任何一个。

然而，在我们这样做之前，值得询问Urbit是什么。这通常是混乱的源泉，因为它是旨在融合在一起的多个交互组件的生态系统。如果您要在ulbit组件集上隐喻地运行2-均值，则它们将干净地分为操作系统（URBit OS）和Identity System（URBit ID）。

NOCK：一种非常低级别的功能编程语言。它在简约的LISP方言和滑雪组合器微积分之间大致一半。在URBIT生态系统中，NOCK是URBit OS运行的虚拟机的机器代码。

Vere：NOCK虚拟机的软件实现（写入C），能够在UNIX环境中运行VM。

嗨：一种更高级别的功能编程语言，其中直接写入URBit OS。这最终会编制到Nock。

Identity System，URBit ID是称为Azimuth点的整数地址（类似于IPv4地址）的分层系统。方位点点与公钥（可变或不断）安全地相关联，并且在该公钥基础设施上建立运行URBit的机器之间的通信。

这些可以累积地由数据类型UINT8，UINT16，UINT32，UINT64和UINT128表示。这些数据类型具有熟悉的标准“限制性图”，熟悉C编程语言，如C：

例如，在其中通过取下半部分（或等效，减少模2 ^ 16）将32位整数被胁迫为16位整数。在这2 ^ n位数据类型中的每一个上都有两个优雅的方法来强加振铃结构：

第一选择是熟悉的一个（在C编程语言中，运算符{+，*， - - - }在z /（2 ^ 2 ^ n）z）中与模块化算法一致。在第二选择中，环加是按位XOR，环乘法稍微复杂地定义。

现在，这些限制性映射如何与URBIT相关？它们在一组方位点上施加部分顺序，其中x≤y如果x是y在限制图下的图像。这种部分顺序的哈斯图图是256棵树的森林，每个森林都有一个在其根的星系。对于不是Galaxy或Comet的每个方位角，此哈列图确定了那个方位角的唯一父级。例如，大多数行星都有明星作为父母。

彗星的父母身份是不同的：彗星的父级是其在限制图UINT128→UINT16下的图像，这必须是愿意主持彗星的五星之一。彗星是公共钥匙的直接散布（所以，与行星不同，不能在不同的所有者之间传输）。

行星，星星和星系是在Ethereum Blockchain上的非娱乐标记的可交易。这给出了从每个方位角点（32位，并且容易难忘）到Etereum地址（160位和加密安全）的可修改的分散映射。因此，可以无信任地验证方位角指向的所有者，并因此设置具有该方位点的安全通信信道;以这种方式建立运行Urbit OS的机器之间的所有通信。

表示方位点点的整数通过以下过程将表示方位点点转换为人类可读名称（称为“@P”）：

对于行星和卫星（不是恒星和星系），将Feistel密码应用于整数的最低32位。这是一种可逆排列，旨在混淆行星和父颗星的名称之间的关系，反映了行星被允许在星空之间自由移动的事实。

生成（加密）整数的字节每个都将每个用于均匀索引字节（后缀）和奇数索引字节（前缀）的单独查找表转换为三个字母的音节。每个音节由两个辅音的侧翼侧翼。

音节用大端编写，在开始时每个16位字和三角形之间的连字符。

32位行星名称的示例是〜sorreg-namtyv，属于urbit的Deposited创始人。

在此StackOverFlow答案中给出了对过程的更全面描述，包括两个256元素音节查找表。

除了发音的'@P'标识符之外，还有一种名为SIGIL的视觉编码。这将在2×2排列的单独象限中存储（加密的！）32位整数的每个字节存储，再次使用一对256元素查找表。这里显示了这个星球的SIGIL：

Gavin Atkinson描述了创建Sigils系统所涉及的设计决策。由于稀缺和审美吸引力的组合，具有圆形SIGIL和/或有意义的@P名称（例如，~~木壁）往往更昂贵的行星往往更加昂贵。

手动填充到象限图块的查找表映射到象限块（通过绘制512瓦设计），因此可以认为URBit Sigils在程序上生成。 [完全程序生成的系统也可能已经有效，例如2009年的这个Wolfram博客文章中的系统，但现在不太可能改变。]这是，仍然是与@P名称高度一致的;还手动填充音节查找表。

nock是这里描述的低级纯功能编程语言。代码和数据只是二进制树（名为名词），其离开是非负整数的。 NOCK解释器是一项机智函数*，其域和Codomain都是名词的空间;它的语义在其自身和其他一元职能方面递归定义。

我对这些函数的最爱是树寻址运算符，/，它定义如下：

/ [1 a] a / [2 ab] a / [3 ab] b / [（a + a）b] / [2 / [ab] / [（a + a + 1）b] / [3 / [ab]] / a / a

特别地，如果我们让L（x）和r（x）引用树x的左和右子树，那么我们有：

用'r'用'l'替换每个'0'（在这个例子中，“rlrrlllllrr”）;

服用x并顺序地将每个字符应用于它（在该示例中，给出r（l（l（l（l（l（l（l（r（r（r（r（r（r（r（x））））））））），注意最外面的函数是最低有效位）。

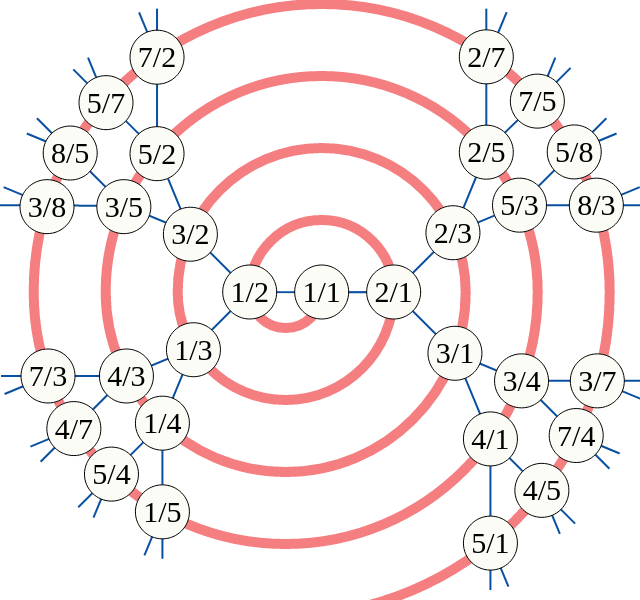
如果我们根据使用/运算符在该节点上扎根于该节点所需的自然数所需的自然数来枚举无限二叉树中的节点，则这与树的广度遍历一致。这与Calkin-Wilf序列与Calkin-Wilf树相同的枚举（下面的鲑鱼螺旋），在该图中显示了David Eppstein：

操作员/是有用的，即LISP分布通常为所有2≤N≤15实现此功能的特殊情况，请参阅作为{CAR，CDR，...，CDDDDDDDDDDDR}。

NOCK，如果天真地评估，将是令人难以置信的低效：递减整数N需要时间成比例。因此，仿真器使用称为喷射的巧妙想法：仿真器模式与各种模式（例如应用于整数的递减函数）并呼叫直接递减整数的运行时优化。

URBit项目成功地实现了整个操作系统内核作为这种语言的函数，由于使用喷气机，它在实践中表现。 Hoon Compiler（将以更高级语言编写的程序编译为低级Nock Language）生成代码，这些代码将成功匹配这些喷射器。

用喷气机，它可能比NOCK更低。 URBIT没有这样做，因为这样做并没有真正的观点，除了在更简单的语言方面给出了NOCK的正式定义：

如果我们选择绝对简单，为什么不全程？它可以在没有型号的Lambda微积分中或在SK组合轨道微积分中实施NOCK。

名词树叶的非负整数可以使用教堂数字来表示：n是将其参数f映射到其n倍函数组合物f ^ n的高阶函数。

然而，遗憾的是，没有一种方法来查询名词是否是整数或一对。因此，我们需要使用稍微更复杂的NOCK名词编码，其中我们标记为每个名词的类型：

用于定义NOCK解释器的机构函数现在可以自行实现为组合器，最多可达和包括NOCK解释器*本身。

例如，问号运算符可以通过拍摄教会对的第一个元素（这是教堂数字0或1），然后将其“拳击”作为一个Noun，而不是'裸露的教堂数字：

在维基百科文章中定义了“对”和“第一”功能的位置。

递增运算符需要取消填写整数，取其后继，然后重新键入：

从技术上讲，我们在这里作弊，因为根据NOCK定义，需要在有序对和整数上定义+（x）。特别是，我们需要使用first（x）来提取教堂数字，指定x是否是有序对或整数和分支：如果教堂数字是1，那么我们可以返回一对（1，supm（第二（X）））;如果教堂数字是0，那么我们需要返回+（x）。通过固定点组合器可以从该递归定义中删除自引用。

剩余的运营商都是递归，因此他们同样需要在其实现中需要固定点组合器。

尝试为SK组合器微积分编写喷射推进的仿真器是一个有趣的练习，包括优化，例如内部代表教堂数字作为整数（具有诸如GMP的库，允许任意大型整数）并使用喷射来调用 适当时GMP实现算术运算。 通过使用“压缩相同的子树”的想法，熟悉散列和库的图书馆来操纵二进制决策图，我们避免过度编码开销，并能够实现诸如递减运算符之类的（标准实现的标准实现）的恒定时间识别。