张拉整体

跳转到导航 跳转到搜索 基于在连续张力网内受压中使用孤立组件的结构原理 张拉整体性、张力完整性或浮动压缩是基于在连续张力网内受压的孤立组件系统的结构原理，并以这样的方式布置，即压缩构件（通常是杆或支柱）不会相互接触，而预应力张拉构件（通常是缆索或钢筋束）在空间上勾勒出系统。 [1] 该术语由巴克敏斯特·富勒在 1960 年代创造，作为“张力完整性”的混合词。 [2] 张拉整体的另一个名称，浮动压缩，主要由建构主义艺术家肯尼思·斯内尔森使用。构件承受纯压缩或纯拉伸，这意味着只有在缆索屈服或杆屈曲时，结构才会失效。这使得每个构件的材料特性和横截面几何形状能够针对其承载的特定载荷进行优化。预载或张拉预应力使缆索始终处于张力状态，以保持结构完整性。机械稳定性，当结构上的应力增加时，允许构件保持拉伸/压缩。随着缆索张力的增加，该结构也变得更硬。由于这些模式，没有结构构件经历弯矩并且系统内没有剪切应力。这可以为它们的质量和部件的横截面产生异常坚固和刚性的结构。加载至少一些张拉整体结构会导致拉胀响应和负泊松比，例如 T3 棱柱和 6 支柱张拉整体二十面体。

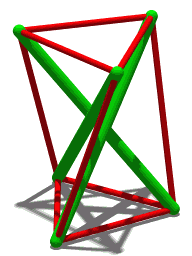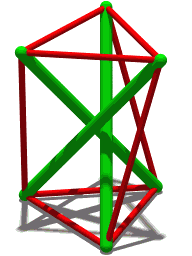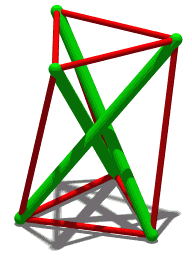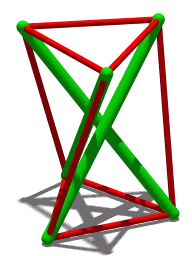
在 1951 年的 Skylon 中可以看到张拉整体的概念性构建块。六根电缆，每端三根，将塔固定到位。连接到底部的三根电缆“定义”了它的位置。其他三根电缆只是保持垂直。三杆张拉整体结构（如右图所示）建立在这个更简单的结构上：每个绿色杆的末端看起来像 Skylon 的顶部和底部。只要任意两根缆索之间的夹角小于180°，就可以很好地确定杆的位置。虽然三根电缆是稳定性的最低要求，但为了美观或增加稳定性，可以将额外的电缆连接到每个节点。例如，Snelson 的 Needle Tower 使用重复模式，该模式使用每个节点连接到 5 根电缆的节点构建。 Eleanor Heartney 指出视觉透明度是这些结构的重要美学品质。 [3] Korkmaz 等。认为轻量级张拉整体结构适用于自适应架构。 [4] [5] 从 1960 年代开始，张拉整体在建筑中的应用有所增加，当时 Maciej Gintowt 和 Maciej Krasiński 设计了 ​​Spodek 竞技场综合体（位于波兰卡托维兹），作为最早采用张拉整体原理的主要结构之一。屋顶使用由支撑其圆周的电缆系统控制的倾斜表面。张拉整体原则也用于大卫·盖格的首尔奥林匹克体操竞技场（1988 年夏季奥运会）和乔治亚圆顶体育场（1996 年夏季奥运会）。坦帕湾光芒队大联盟棒球队的主场 Tropicana Field 也有一个由大型张拉整体结构支撑的圆顶屋顶。 2009 年 10 月 4 日，Kurilpa 大桥在澳大利亚昆士兰州布里斯班河上通车。它是一种基于张拉整体原理的多桅杆斜拉结构，是目前世界上最大的张拉整体桥梁。自 2000 年代初以来，张拉整体也吸引了机器人专家的兴趣，因为它们具有设计轻型和弹性机器人的潜力。许多研究调查了张拉整体漫游车、仿生机器人和模块化软机器人。最著名的张拉整体机器人是 Super Ball，[6] 是一种使用 6 杆张拉整体结构进行太空探索的漫游车，目前正在 NASA Ames 开发。 Biotensegrity 是 Stephen Levin 博士创造的一个术语，是张拉整体原理在生物结构中的应用。 [7] 生物结构，如肌肉、骨骼、筋膜、韧带和肌腱，或刚性和弹性的细胞膜，通过拉伸和压缩部分的统一而变得坚固。肌肉骨骼系统在肌肉和结缔组织的连续网络中保持张力 [8]，而骨骼提供不连续的压缩支撑。即使是乍一看就像一堆椎骨相互靠在一起的人体脊柱，实际上也是一个张拉整体结构。 [9]

Donald E. Ingber 开发了张拉整体理论来描述分子生物学中观察到的众多现象。 [10] 例如，细胞的表达形状，无论是它们对施加压力的反应，与底物的相互作用等，都可以通过将细胞的细胞骨架表示为张拉整体来进行数学建模。此外，在将张整体原理应用于化合物、蛋白质的自发自组装的基础上，也可以理解在自然界中发现的几何图案（DNA 的螺旋、涡旋的测地圆顶、巴克敏斯特富勒烯等），[11]甚至器官。这种观点得到了张拉整体的拉压相互作用如何最大限度地减少保持稳定性和实现结构弹性所需的材料的支持。 [12] 因此，自然选择压力可能有利于以张拉整体方式组织的生物系统。这些结构中的受拉构件——无论是富勒的圆顶还是斯内尔森的雕塑——绘制了相邻构件之间的最短路径（因此，根据定义，按测地线排列）。张力在两点之间的最短距离上自然地传递，因此张拉整体结构的成员被精确定位以最好地承受应力。出于这个原因，张拉整体结构提供了最大的强度。 [10] 在胚胎学中，Richard Gordon 提出胚胎分化波由“分化细胞器”[13] 传播，其中细胞骨架组装在细胞顶端的双稳态张拉整体结构中，称为“细胞状态分离器”。 [14] 张拉整体的起源是有争议的。 [16] 许多传统结构，例如皮划艇和 shōji，以类似的方式使用拉伸和压缩元件。 1948 年，艺术家肯尼斯·斯内尔森 (Kenneth Snelson) 在黑山学院（巴克明斯特·富勒 (Buckminster Fuller) 曾在那里授课）和其他地方进行了艺术探索后，创作了他的创新“X 片”。几年后，“张拉整体”一词是由富勒创造的，他以他的测地圆顶而闻名。在他的整个职业生涯中，富勒一直在尝试在他的作品中加入拉伸组件，例如在他的 dymaxion 房屋的框架中。 [17] Snelson 1948 年的创新促使Fuller 立即委托Snelson 制造桅杆。 1949 年，富勒基于该技术开发了张拉整体二十面体，他和他的学生迅速开发了进一步的结构并将该技术应用于建造圆顶。在中断之后，Snelson 还继续创作了大量基于张拉整体概念的雕塑。他的主要作品始于 1959 年，当时在现代艺术博物馆举办了一场重要展览。在 MOMA 展览上，富勒展示了桅杆和他的一些其他作品。 [18] 在这次展览中，Snelson 在与富勒和展览组织者就桅杆的功劳进行了讨论后，还在玻璃橱窗中展示了一些作品。 [19] 俄罗斯艺术家 Viatcheslav Koleichuk 声称张拉整体的概念是由拉脱维亚血统的苏联前卫艺术家 Kārlis Johansons (lv) 发明的，他为 1921 年俄罗斯建构主义的主要展览贡献了一些作品。Koleichuk 的主张是玛丽亚·高夫为 1921 年建构主义展览的其中一件作品提供了支持。 [21] Snelson 承认建构主义者对他的工作有影响（询问？）。 [22] 法国工程师 David Georges Emmerich 也注意到 Kārlis Johansons 的作品（和工业设计理念）似乎预见了张拉整体概念。 [23]

三杆张拉整体结构（三向棱镜）具有以下特性：对于给定（公共）长度的受压构件“杆”（共有三个）和给定（公共）长度的受拉索“筋”（总共六个）将杆端连接在一起，连接杆顶部与相邻杆底部的筋的（公共）长度有一个特定值，使结构保持稳定的形状。对于这样的结构，很容易证明由杆顶形成的三角形和由杆底形成的三角形相对于彼此旋转了 5π/6（弧度）的角度。 [24] Sultan 等人分析了几个 2 级张拉整体结构的稳定性（“预应力”）。 [25] 张整体二十面体，由 Snelson 于 1949 年首次研究，[26] 在称为 Jessen 二十面体的多面体的边缘具有支柱和筋。这是一个稳定的结构，尽管具有无限小的流动性。 [27] 要看到这一点，请考虑以原点为中心、边长为 2 d 的立方体。在每个立方体面的平面上放置一个长度为 2 l 的支柱，使每个支柱平行于面的一个边缘并在面的中心。此外，每个支柱应平行于立方体相反面上的支柱，但与所有其他支柱正交。如果一个支柱的笛卡尔坐标是 ( 0 , d , l ) {\displaystyle (0,d,l)} 和 ( 0 , d , − l ) {\displaystyle (0,d,-l)} ，那些它的平行支柱将分别是 ( 0 , − d , − l ) {\displaystyle (0,-d,-l)} 和 ( 0 , − d , l ) {\displaystyle (0,-d,l) } .其他支柱末端（顶点）的坐标通过排列坐标获得，例如， ( 0 , d , l ) → ( d , l , 0 ) → ( l , 0 , d ) {\displaystyle (0,d, l)\rightarrow (d,l,0)\rightarrow (l,0,d)}（立方体主对角线上的旋转对称）。任意两个相邻顶点 (0, d, l) 和 ( d, l, 0) 之间的距离 s 为 s 2 = ( d − l ) 2 + d 2 + l 2 = 2 ( d − 1 2 l ) 2 + 3 2 l 2 {\displaystyle s^{2}=(dl)^{2}+d^{2}+l^{2}=2\left(d-{\frac {1}{2}}\ ,l\right)^{2}+{\frac {3}{2}}\,l^{2}} 想象一下这个图是由给定长度 2 l 的支柱和给定长度 s 的肌腱（连接相邻顶点）构建的, s > 3 2 l {\displaystyle s>{\sqrt {\frac {3}{2}}}\,l} 。该关系告诉我们 d 有两个可能的值：一个是通过将支柱推到一起来实现的，另一个是通过将它们拉开来实现的。在特殊情况下 s = 3 2 l {\displaystyle s={\sqrt {\frac {3}{2}}}\,l} 两个极端重合，并且 d = 1 2 l {\displaystyle d={\ frac {1}{2}}\,l} ，因此该图形是稳定的张拉整体二十面体。这种参数选择为顶点提供了 Jessen 二十面体的位置；它们不同于正二十面体，对于正二十面体，d {\displaystyle d} 和 l {\displaystyle l} 的比率将是黄金比例，而不是 2。然而，这两组坐标都位于一个连续的位置系列中，范围从立方八面体到八面体（作为极限情况），由 HSM Coxeter [28] 描述，后来被 Buckminster Fuller 称为“jitterbug 运动”。 [29] [30] 由于张拉整体二十面体代表上述关系的极值点，它具有无穷小的流动性：肌腱长度 s 的微小变化（例如通过拉伸肌腱）会导致距离的更大变化2 d 的支柱。

由花园木桩和尼龙绳制成的张拉整体圆顶，建在房子的院子里，2009 年消散，沙漏塔艺术雕塑，包括张拉整体结构，在 AfrikaBurn 建造，2015 年，火人节区域活动 ^ Eleanor Hartley，“Ken Snelson and the结构美学”，在肯尼思·斯内尔森的马尔堡画廊目录中：精选作品：1948-2009，展出时间为 2009 年 2 月 19 日至 3 月 21 日。^ Levin, Stephen（2015 年）。 “16. 张拉整体，新生物力学”。在哈特森，迈克尔；沃德，亚当（编辑）。牛津肌肉骨骼医学教科书。牛津大学出版社。第 155-56、158-60 页。 ISBN 978-0-19-967410-7。 ^ Levin, Stephen M.（2002 年 9 月 1 日）。 “张拉整体桁架作为脊柱力学模型：生物张拉整体”。医学和生物学力学杂志。 02 (3n04): 375–88。 doi：10.1142/S0219519402000472。 ISSN 0219-5194。 ^ ab Ingber, Donald E.（1998 年 1 月）。 “生命的建筑”（PDF）。科学美国人。 278（1）：48-57。 Bibcode：1998SciAm.278a..48I。 doi：10.1038/scientificamerican0198-48。 PMID 11536845。2005 年 5 月 15 日从原始文件 (PDF) 存档。^ Edwards, Scott A.;瓦格纳，约翰内斯；格雷特，弗劳克 (2012)。 “球状蛋白质中的动态预应力”。 PLOS 计算生物学。 8 (5): e1002509。书目代码：2012PLSCB...8E2509E。 doi：10.1371/journal.pcbi.1002509。 PMC 3349725。PMID 22589712。

^ 斯凯尔顿，罗伯特 (2016)。 “全局稳定的最小质量压缩张拉整体结构”。复合结构。 141：346-54。 doi：10.1016/j.compstruct.2016.01.105。 ^ 戈登，娜塔莉 K.；戈登，理查德（2016 年）。 “胚胎分化的细胞器：细胞状态分裂器”。理论生物学和医学建模。 13: 11. doi: 10.1186/s12976-016-0037-2。 PMC 4785624。PMID 26965444。^ Gordon, Richard (1999)。分层基因组和分化波。数学生物学和医学丛书。 3. doi：10.1142/2755。 ISBN 978-981-02-2268-0。 ^ Gómez-Jáuregui, V. (2009)。 “有争议的张拉整体性起源”（PDF）。国际空间结构协会 IASS 研讨会 2009，瓦伦西亚。 ^ 见富勒在他 1961 年为投资组合和艺术新闻年刊（第 4 号）发表的关于张拉整体性的文章中本次展览的照片。 ^ David Georges Emmerich，Structures Tendues et Autotendantes，巴黎：巴黎拉维莱特建筑学院，1988 年，第 30-31 页。 ^ 苏丹，康奈尔；马丁·科利斯；罗伯特·E·斯凯尔顿 (2001)。 “张拉整体结构的预应力问题：一些解析解”（PDF）。国际固体与结构杂志。 26: 145. 2015 年 10 月 23 日从原件 (PDF) 存档。

^ Cera, Angelo Brian Micubo (2020)。电缆驱动柔性张拉整体机器人的设计、控制和运动规划（博士论文）。加州大学伯克利分校。页。 5. ^ Coxeter, HSM (1973) [1948]。 “3.7 规则和准规则实体顶点的坐标”。规则多面体（第 3 版）。纽约：多佛。第 51-52 页。 ^ Verheyen, HF (1989)。 “一套完整的 Jitterbug 变压器及其运动分析”。计算机与数学与应用。 17, 1-3 (1-3): 203-250。 doi：10.1016/0898-1221(89)90160-0。 Fuller, R. Buckminster (1961)。 “张拉整体性”。作品集和艺术新闻年刊 (4)：112–127、144、148。—； Marks, Robert W. (1973) [1960]。 Buckminster Fuller 的 Dymaxion 世界。锚书。无花果。 261-280。 ISBN 978-0385018043。从富勒的角度对张拉整体的范围进行了很好的概述，并且在大多数情况下对早期结构进行了有趣的概述，并对其进行了仔细的归因。 Gómez-Jáuregui, Valentin (2007)。 Tensegridad。 Estructuras Tensegríticas en Ciencia y Arte（西班牙语）。桑坦德：坎塔布里亚大学。 ISBN 978-84-8102-437-1。 ——（2010 年）。张拉整体结构及其在建筑中的应用。桑坦德：坎塔布里亚大学公共服务。 ISBN 978-84-8102-575-0。

高夫，玛丽亚（1998 年春季）。 “在建构主义实验室：卡尔·伊奥甘森的冷结构”。十月。 84：90-117。 doi：10.2307/779210。 JSTOR 779210。胡安，SJ； Tur, JM（2008 年 7 月）。 “张拉整体框架：静态分析回顾”。机制和机器理论。 43（7）：859-81。 CiteSeerX 10.1.1.574.7510。 doi：10.1016/j.mechmachtheory.2007.06.010。科克马兹，思南；贝尔哈吉阿里，尼扎尔；史密斯，伊恩 FC（2011 年 6 月）。 “确定主动张拉整体结构的损伤容限控制策略”(PDF)。工程结构。 33（6）：1930-1939。 CiteSeerX 10.1.1.370.6243。 doi：10.1016/j.engstruct.2011.02.031。 2011 年 9 月 29 日从原件 (PDF) 存档。—； ——； —（2012 年 1 月）。 “张拉整体桥梁损伤容限控制系统的配置”。高级工程信息学。 26 (1): 145–155。 doi：10.1016/j.aei.2011.10.002。拉瓦尼，哈雷什，编辑。 (1996)。 “张拉整体的起源：Emmerich、Fuller 和 Snelson 的观点”。国际空间结构杂志。 11 (1–2): 27–55。 doi：10.1177/026635119601-204。 S2CID 114004009. Souza, Thales R.;丰塞卡，塞尔吉奥 T.；贡萨尔维斯，加布里埃拉 G.；陶笛，朱莉安娜 M.；曼奇尼、玛丽莎 C.（2009 年 10 月）。 “踝关节被动共同张力显示的预应力”。生物力学杂志。 42 (14): 2374–80。 doi：10.1016/j.jbiomech.2009.06.033。 PMID 19647832。福布斯，彼得 (2010) [2006]。 “9. 推拉式建筑系统”。壁虎的脚：科学家如何从自然的书中摘下一片叶子。哈珀柯林斯。第 197-230 页。 ISBN 978-0-00-740547-3。

Hanaor, Ariel (1997)。 “13. 张拉整体：理论与应用”。在 Gabriel, J. François (ed.)。超越立方体：空间框架和多面体的架构。威利。第 385-408 页。 ISBN 978-0-471-12261-6。休肯纳 (1976)。测地线数学及其使用方法。加州大学出版社。 ISBN 978-0520029248。 2003 重印 ISBN 0520239318。这是学习张拉整体数学和建筑模型的良好起点。马西奇，米连科；斯凯尔顿，罗伯特 E。 Gill, Philip E.（2005 年 8 月）。 “代数张拉整体找形”。国际固体与结构杂志。 42 (16–17): 4833–4858。 doi：10.1016/j.ijsolstr.2005.01.014。他们提出了一个显着的结果，即张拉整体的任何线性变换也是张拉整体。摩根，GJ（2003 年）。 “历史回顾：病毒、水晶和测地圆顶”。生化科学趋势。 28 (2): 86-90。 doi：10.1016/S0968-0004(02)00007-5。 PMID 12575996。Motro, R. (1992)。 “张拉整体系统：最先进的技术”。国际空间结构杂志。 7 (2): 75–84。 doi：10.1177/026635119200700201。 S2CID 107820090。Pugh, Anthony (1976)。张拉整体介绍。加州大学出版社。 ISBN 978-0-520-03055-8。 2008 年 5 月 4 日从原件存档。维尔奈，奥伦 (1990)。 Cable Nets and Tensegric Shells：Analysis and Design Applications，纽约：Ellis Horwood Ltd. [ISBN 缺失]

王斌兵（1998）。 “索杆系统：第一部分——张拉整体”。建筑钢研究杂志。 45 (3): 281–89。 doi：10.1016/S0143-974X(97)00075-8。瑞士联邦理工学院 (EPFL)、应用计算和力学实验室 (IMAC) 的张拉整体领域的科学出版物 Stephen Levin 的 Biotensegrity 网站 几篇骨科医生撰写的关于从病毒到脊椎动物的生物结构张拉力学的论文。