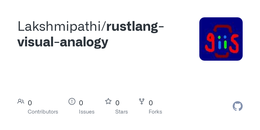
所有权公式
管理复杂IT基础设施的团队通常由全职员工(FTE和#39;s)和连续工人(又名承包商)组成。承包商太多而FTE不足的团队';这种方法通常是无效的。FTE和#39太多的团队;没有足够的承包商是有效的,但代价高昂。什么是正确的平衡?我开始思考,我是否能够想出一个方程式,来模拟与FTE混合的团队的效率';他和承包商一起设计了一个模型,我';我们边走边解释。
警告:这是伪科学,基于一个人#39;她对与许多不同类型的团队合作的观察。请不要把它当作科学真理。
这种模式的前提是,承包商有一种奇怪的倾向,即在复杂系统的“所有权”问题上苦苦挣扎。那里';系统运行状况与FTE数量之间的相关性';这其中涉及到了许多问题。我的理论是FTE';s、 从本质上讲,他们更倾向于拥有一个“端到端”的系统,因为他们';我们将长期参与其中。他们';我们更愿意做工作以外的事情,以保持系统良好的维护。例如,联系利益相关者/客户并召开会议,思考系统故障模式并规划缓解策略,重新设计稳定的系统以提高效率等。另一方面,承包商更容易实现其工作范围内的预定义目标。这并不奇怪,因为这正是他们得到报酬的目的!像FTE和#39一样行事的承包商;don#39;I don’我不会在这里呆很长时间。他们要么被赞助公司雇佣,要么被重新分配到另一个赞助商,以扑灭另一个账户的火灾。
总而言之,我不';我不认为这个系统有什么问题,只要它得到有效利用。一个复杂的系统需要将军和士兵共同有效运作。承包商所做的工作通常是FTE';s唐';我不想做FTE';s do是承包商认为超出其范围的工作。复杂的系统需要所有权因素,而承包商无法单独提供所有权因素。
因此,为了让领导层在复杂系统周围维持长期运行、稳定、经济高效的团队,他们必须接受这些自然规则,并据此进行规划。经过对这个体系的基本真理的深思熟虑,我';我们得出了以下结论:
例如,如果你有一个中等复杂的系统,你觉得可以由5名工程师充分覆盖。我们';我们称之为5个所有权单位。你能通过加入承包商以更便宜的方式提出5套所有权单元吗?也许我们可以用数学术语来优化这个系统:
许多承包商靠自己的力量接近于提供完全所有权,但永远无法达到完全所有权单位。
更多全职员工';提高承包商的有效性。换句话说,当FTE和#39较多时,承包商提供更多的所有权单位;这牵涉其中。
我相信下面的公式可以很好地模拟一个混合团队中你能期望的有效团队人数。
其中y是全职员工的数量,x是承包商的数量
让';让我们把它分解开来,更详细地检查零件。首先,总有效所有权员工数应为FTE员工数加上承包商有效性的一些修饰符之和,可以表示为x(?)+y、 那么,我们如何确定有效性呢?经过深思熟虑之后,很明显,我需要一个数学方程式,它可以接近,但永远不会是1。如果组合中没有全职员工,它也必须为零。此外,如果FTE的比例很高,则需要“提高”FTE#39;这是给承包商的。因此,使用了这个公式,即I';我称之为“承包商系数”或“cc”
让';让我们看一个简短的数据表来解释它#39;s对承包商总有效人数的影响:
我';我的数学不够好,无法解决这个问题(如果你有所有的FTE,那么你无论如何也不需要这个公式)
现在我们有了一个合理的有效员工数公式,我们可以轻松地修改它,以找到不同组合的总拥有成本:
其中,j是承包商工资,k是员工工资,x是承包商数量,y是员工数量。
使用这两个公式,让';让我们插入一些数字并检查数据表。
当FTE与承包商的比例在1:1到2:1之间时,团队最有效,但在5:4的比例下最有效。
当然,这种模式存在已知的局限性。首先,有一些非常非常好的承包商和一些非常糟糕的全职员工';它可以把这个扔掉。然而,随着时间的推移,这些案例往往会在组织之外自行解决。此外,成本不同,效率也会有很大差异。一些非常昂贵的承包商几乎可以被FTE取代';这取决于它们有多贵。然而,即使是非常昂贵的承包商也只能“拥有”这么多。
我';I&#I';我现在就把这件事留着做。
另外,关于Wolfram Alpha的情节很有趣。我';我还要解y和x的方程,以确定最小/最大值,从而确定最有效的比率。
其中y是全职员工的数量#39;s、 x是承包商数量,110是FTE工资(单位:千美元/年),70是承包商工资(单位:千美元/年)
*得出这一结论的方法是,提出一个粗略的公式来描述我的观察结果,然后插入已知现实团队的人数,以及我对这些团队有效性的感知。如果结果与我的经验不符,那么我会调整公式,直到它更接近我的经验。然后我加入了一些极端的边缘案例,确保它听起来仍然正常。