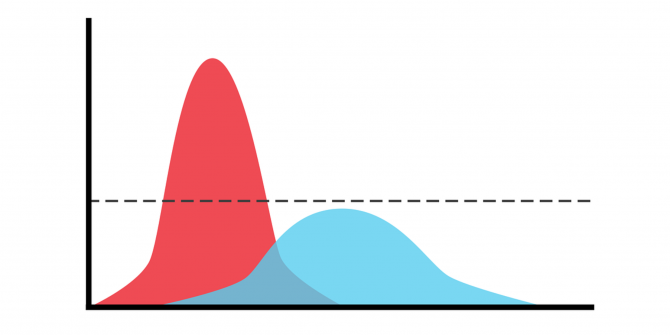
公众不了解用来描绘冠状病毒的对数曲线图。

大众媒体通常在对数图上描绘有关冠状病毒死亡的信息。但是他们的读者理解他们吗？亚历山德罗·罗曼诺(Alessandro Romano)、基亚拉·索蒂斯(Chiara SoTis)、戈兰·多明尼奥尼(Goran Dominioni)和塞巴斯蒂安·吉迪(Sebasián Guidi)进行了一项实验，结果表明他们没有这么做。或许更相关的是：看着线性标度图的受访者对流行病的态度和政策偏好与那些在对数图上显示相同数据的人不同。因此，仅仅改变数据呈现的规模就可以改变公共政策的偏好和担忧的程度，即使在人们经常接触到大量冠状病毒相关信息的时候也是如此。基于这些发现，他们呼吁媒体和政府机构使用线性标度图。

事实上，信息的框架可以戏剧性地改变我们对它的反应，这一事实几乎不会让本博客的任何读者感到惊讶。顺便说一句，框架效应的典型例子涉及一种流行病：一种600人中有200人死亡的疾病被认为比400人存活的疾病更糟糕。虽然这场想象中的流行病只是一次思想实验，但一场真正的全球大流行最终被证明是一个不幸的框架效应实验室。在最近的一次实验中，我们展示了框架是如何对人们对冠状病毒信息拼图中最重要的组成部分之一：死亡人数的反应产生至关重要的影响的。我们表明，媒体通常用来显示这一信息的对数比例图很难被公众理解，并影响到人们对大流行的态度和政策偏好。这一发现具有重要意义，因为在大流行期间，公众甚至比往常更依赖媒体传达可理解的信息，以便就健康保护行为做出知情决定。

许多媒体使用对数刻度图描述有关冠状病毒病例和死亡人数的信息。乍一看，这似乎是明智之举。事实上，他们中的许多人通过展示这些图表在传达关于传染病指数性质的信息方面要好得多来为自己的决定辩护。对于历史爱好者来说，广受欢迎的经济学家欧文·费舍尔(Irving Fisher)也相信这一点，这导致他在1917年强烈倡导使用它们(就在西班牙流感使它们变得悲剧性之前)。费舍尔对这个规模欣喜若狂：“一旦习惯了，就不会误导。”然而，事实证明，即使是专业的科学家也不习惯这样做。不足为奇的是，普通公众也是如此。

我们进行了一项受试者之间的实验，以测试人们是否更好地理解了对数尺度或线性尺度下的图表，以及图表显示的尺度是否会影响他们的担忧程度和政策偏好。在我们的n=2000名美国居民样本中，有一半在调查时被展示了美国与冠状病毒相关的死亡的进展情况，并以对数标度绘制。另一半则收到了完全相同的信息--这一次是用一个很好的老式线性标尺绘制的。

与费舍尔的乐观相反，我们发现，在对数尺度上阅读信息的那组人对图形的理解水平要低得多：只有40.66%的人能正确回答关于图形的基本问题(一周或另一周死亡人数是否更多)，相比之下，在线性尺度上的受访者比例为83.79%。此外，事实证明，对数组的人在预测大流行的演变方面也更差：他们在实验进行后的一周内平均预测了71,250人死亡，而线性组预测的死亡人数为63,429人(我们的ARIMA预测模型显示55,791人，而当天的实际死亡人数为54,256人)。尽管如此，两组受访者对自己的答案都表示了相似的信心。

此外，我们测试了所使用的量表是否影响了受访者对大流行的态度。看起来是这样的。首先，我们发现，尽管预测的死亡人数会更高，但看到对数刻度图的人声称对冠状病毒引起的健康危机不那么担心。

然而，分歧并不止步于此。他们看到的图表的规模影响着人们对他们的政策偏好和既定行为的反应。在其他情况相同的情况下，看到线性标度图上信息的受访者对关闭非必要企业的政策的支持程度低于那些看到对数标度图的受访者-尽管他们也倾向于稍后重新开放这些企业。与此同时，那些看到线性图表的人更愿意支持一项旨在为公民提供面具的假想的州级税收。

对我们的发现的一种可能的解释是，线性规模给人的印象是大流行日益严重，没有任何改善的迹象。同时，曲线上的对数

诚然，我们不知道哪些政策偏好更优越。然而，我们确实知道，与那些看到对数刻度图的人不同，接触线性刻度图的人可以根据他们更好地理解的信息形成他们的偏好。这是一个足够充分的理由，表明大众媒体和政策制定者应该总是使用线性尺度的图表来描述大流行的演变，或者至少他们应该同时显示两个尺度。毕竟，如果我们想让人们洗手并保持6英尺的距离，他们就会更好地了解正在发生的事情。

这篇文章代表了作者的观点，而不是冠状病毒博客或伦敦证交所的观点。*实验的预印本可以在这里找到，相应的作者可以通过[email protected]联系到。

我们的教育系统似乎系统地愚弄了公众--尤其是在数学和历史科目上。如果我被阴谋论所吸引，我可能会认为，一个不会计算的公众，忘记了20多年前学到的任何教训，使得官僚霸权对技术官僚…来说特别容易。

谢谢您的评论！我们喜欢看杯子半满的样子。当呈现线性标尺时，人们对图表有很好的理解，并做出了准确的预测。我们只是认为原木规模可能会令人困惑，正如之前的研究(Menger等人)所表明的那样。2018年，在文章中链接)。

我要反驳这一点，我想说，这并不是说我们的教育制度让公众变得愚蠢，而是它对学生的非线性思维教育不足。人类本质上是线性的、因果的思考者，除非被教导如何去做，更重要的是，非线性思维在现实世界中有多么重要，否则走出这一领域是有点陌生的。

不过，你能澄清一下这一说法吗：“看到线性标度图上信息的受访者对关闭非必要企业的政策的支持程度低于那些看到对数标度图的受访者”，这似乎与以下说法相矛盾：“对我们的发现，一种可能的解释是，线性标尺给人的印象是，流行病正在蔓延，没有任何改善的迹象。”

后者难道不意味着那些阅读线性图的人应该*更强烈地支持关闭非必要企业的政策吗？还是我漏掉了什么明显的东西？

非常感谢您的客气话！你提出了一个非常好的观点。为了提高透明度，我们预先登记了我们所做的所有假设。虽然调查结果的总体方向与我们的想法一致，但一些结果是出乎意料的。这就是其中之一，这就是为什么我们在博客文章中也标记了它。我们对这一发现的解释是，线性刻度给人的印象是某种东西将持续很长一段时间，因为它看起来不像是“平坦的”曲线。因此，由于经济不可能冻结多个月，人们可能会认为，还是早点重新开放为好。换句话说，如果你告诉某人，通过关闭经济两个月就可以遏制病毒，他们很可能会支持关闭。然而，如果你告诉他们，我们需要关闭经济两年才能看到改善，他们可能更愿意保持经济开放，并采取其他遏制战略。诚然，这只是我们对结果的解读，而不是我们可以根据我们的数据进行测试的东西。最好的，基亚拉

嗨，理查德！谢谢你的评论。我们并不清楚人类是否天生就是“线性的”(不乏证据表明，儿童和非西方成年人直观地将数字绘制在对数而不是线性的尺度上：https://science.sciencemag.org/content/sci/320/5880/1217.full.pdf等)。进一步测试人们是如何理解对数增长的，以及“线性”教育在多大程度上干扰了对数增长，这确实是非常有趣的。但就我们的结果而言，无论是自然还是教育，看起来线性标度图有助于更好地了解冠状病毒的传播。

我想这在很大程度上取决于你想描绘什么。如果你想吓唬公众，就用线性，如果你想让人放心，就用对数。

如果你想让你的读者了解问题的严重性，你需要根据人口来衡量。与正常的死亡人数相比，4万人的死亡人数是多还是少？

谢谢你的评论！我们完全同意你的意见。这正是我们想提出的问题。没有“中立”的方法来框定数据。呈现总数与按人口比例显示数字的效果将是一个非常有趣的实验，而且非常容易实现！

我们完全同意你的意见。这正是我们想提出的问题。在图表上绘制数据没有“中立”的方法。测试呈现总数与按人口缩放的数字的效果也是非常有趣的。这也很容易做到！

谢谢你的分析。这是非常需要的。作为一家主要报纸的前信息图表编辑，我一直认为我的长处之一是缺乏数学技能。如果我能看懂图表，或许读者也能。是的，我从来没有用过日志图表。同样，始终包含零线或表示它不存在。为公众绘制海图的两条基本规则。

感谢您对我们的工作感兴趣！我们真的很感谢你的话，因为我们没有任何与报纸合作的经验，所以很高兴知道我们提出的观点与在一家主要报纸工作的人产生了共鸣！

我担心，更好地理解线性图形的发现可能更多地说明了用于测试理解能力的问题的选择，而不是关于线形图天生的优越性。

据我所知，所有三个“理解”问题都在测试大致相同的东西：参与者观察一周内变化速度的能力。人们会期望这里的线性图能得到更好的结果--比较两个坡度非常容易，或者可以很容易地外推一个短距离的坡度。(我还要注意，在感兴趣的范围内，线性图以10k为间隔标记，而对数图在10k和100k之间没有任何标记。)。

但还有其他问题可能同样重要。例如，在给定的时间点之后，行为的改变是否减缓了传播速度？我们预计未来“四周”的数字是多少？在这个时间尺度上，曲线的非线性性质变得比一周的预测要重要得多？

对于这两个问题，我怀疑观看对数图表的受试者可能会做得更好(特别是在y轴上有更多的标记)。但这些问题并不涵盖这一领域。

嗨，杰弗里。谢谢你非常有趣的评论！这是很好的思考食粮。我们不能排除被显示为日志的人在处理不同的一组问题或不同的日志刻度图时表现更好。我们试着问一些我们认为相关的问题。例如，一个人明天的行为可能更多地受到她的短期预测(一周)的影响，而不是她的中期预测(四周)。此外，我们从一个广泛使用的网站(https://www.worldometers.info/))中选取了一张图表，以增加外部效度。但我们会非常好奇地看到研究提出了不同的问题。例如，当在图形上绘制多条曲线时会发生什么情况？一些报纸，如英国“金融时报”，就是这样做的。我们也同意，图表有很多细节可以影响人们对它的反应。您在Y轴上的值的示例就是一个很好的例子。然而，人们可以想象，如果人们没有正确理解图表的内容，他们更容易受到图表功能的影响。因此，一种可能的说法是，应该使用易于理解的图表，因为我们无法预测图表的所有细节对人们心理的影响。

关于成人算术的很好的洞察力&令人眼花缭乱。我也一直在博客上谈论这一点，以及公众对Covid问题的理解。您可以在上查看我在4月份举办的3个在线研讨会。https://publiclinguist.blogspot.com/2020/04/lost-in-covid-numbers-weve-picked-most.html?m=1。

我发现的一件事是，图形、图表的介绍性框架有助于读者如何接近视觉数组，以及他们希望找到什么。这最终会影响文本的可读性/可用性。例如，使用当前的情况，纽约市居民可以在网上查看每日发病率和死亡率数字(COVID)，他们在查看条形图之前会看到下面的介绍性声明：“这个图表显示了自2月29日以来COVID 19每天按诊断日期、住院治疗、日期和死亡日期划分的确诊病例数量。”

在语言学中，我们将这些引言称为某种“高级前置陈述”，它向读者发出信号，“准备好阅读关于……的内容”。但在这种情况下，前置陈述是一种打包的方式。我们发现更多有限的、直接的前置陈述会影响理解。你有没有在你的作品中看到过这种框架。图表是如何呈现的？

再次感谢克里斯蒂娜！我们确实有你们所说的前置陈述，来向受访者解释他们会看什么，并解释使用的标尺。然后我们减少了后面问题的解释，但每个问题的图表都附有一条简短的声明。为了增加外部有效性，这些解释非常接近“纽约时报”在文章中提出的解释。然而，我们真的不是语言学专家。我们同意您的观点，即研究不同的框架如何影响理解和政策偏好将是非常有趣的。我们应该谈谈这件事！

以下是我在创建图形的标题和引言/序言时提出的一些问题：

-标题不需要进一步的介绍文本就足够了吗？-不要在介绍中重复任何在图形中清晰和明显的内容。-如果可能，使用短语而不是完整的句子来保持文本简短。-不要使用额外的词语，如“此图形显示”。我们知道这是一幅图画。我们知道它应该显示一些东西。-如果引言超出了一两个简短的短语，请后退一步，询问为什么需要解释图形。最好的图形只需要很少的设置(如果有的话)。大量设置可能表明图形中可能存在严重缺陷。-考虑上下文/设置。如果图片是独立的、被共享的，那么对介绍的需求可能比嵌入在故事中而不打算在真空中消费的需求更大。

我在这方面经常失败。我变得喋喋不休。这就是向不熟悉这项工作的人展示图片以获得原始反应的关键所在。如果他们不能迅速领会它的意图和意义，我就知道我有问题了。人们不应该破译一张信息图，就像我们期望他们破译一篇文章一样。

看看塔夫特举着的“拿破仑进行曲”，它是有史以来最好的信息图表之一。一个对历史知之甚少的漫不经心的观察者甚至可以在不理解创作语言的情况下收集图形方法、范围和粗略的结论。是的，有一个很长的引言，但它是累加性的，不是关键的。https://www.edwardtufte.com/tufte/posters。

这一切都很棒，谢谢！(拿破仑的曲线图很漂亮)正如基亚拉上面所说，我们试图尽可能地模仿我们在报纸上实际使用的介绍(同时也注意对称)。也就是说，在这些图表和介绍中有很多我们不可能做的有趣的事情需要测试，但是如果您有任何想法，我们可以讨论一下！

你有没有在并排显示“两个”图表后测试理解能力？这可能会提高理解能力吗？每种情况都是分开呈现的。

此外，如果图表显示了可比较的数据(例如，您链接的VOX文章中讨论的各国死亡率)，您预计会看到什么影响？你认为会有较小的影响吗？

在得出“公众不理解对数图”的结论之前，这两个都是需要探索的重要假设。

嗨，克里斯汀，这些都是很棒的问题。我们考虑增加两个量表的处理，但最后我们选择了更大的样本量来增加我们的统计能力。我们最初的假设是，看到这两个图表的人只会依赖线性标尺，或者至少我们没有办法测试这一点。当然，我们不知道这一假设是否正确，我们希望未来的研究能对其进行调查。当单个图表显示可比较的数据时，测试会发生什么也会非常有趣。我们的其中一个关于理解的问题实际上显示了两条曲线(男性和女性感染了一种假设的疾病，我们借用了之前关于图形理解的研究)，它还表明，绝大多数读者更好地理解线性标尺，而不是对数标尺。我们不能排除某些特定的问题(即，“A国的感染人数何时能赶上B国的感染人数”)在对数尺度上会有更好的记录--测试它会很棒。但是，让我们假设情况是这样的：当我们有证据表明他们没有很好地理解它的构件(即，单独的曲线)时，我们在什么意义上说他们“理解”了这个图呢？无论如何，出于外部有效性的原因，我们最终决定选择一条曲线：我们调查的大多数报纸都显示了一种国家曲线，其中许多都是对数尺度的。换句话说，我认为目前我们可以得出这样的结论(有一些证据表明)“公众没有很好地理解对数图”，这并不意味着他们在任何情况下都不理解它们，或者无论他们收到多少额外的线索。事实上，正如您所说，未来的研究可能会显示“公众不理解对数图，除非与线性刻度图一起显示/除非它们显示多条曲线之间的比较。”

很抱歉没有时间看完所有的评论，所以我可能会重复。

然而，我只是觉得不可能相信“专门的科学家”不能完全理解半对数图，或者任何人发现推断hig的纵坐标更容易。

..