新冠肺炎：超额死亡率统计数据及其在各国之间的可比性

超额死亡率是相对于通常预期的各种原因造成的死亡人数。在大流行中，死亡人数急剧上升，但原因记录往往不准确，特别是在没有广泛可用的可靠测试的情况下。因此，归因于新冠肺炎的死亡人数可能被严重低估。超额死亡数据克服了报告新冠肺炎相关死亡的两个问题。避免了新冠肺炎相关死亡的误诊或漏报造成的误算。超额死亡率数据包括其他健康状况造成的“附带损害”，如果卫生系统因新冠肺炎病例而不堪重负，或者是由于故意将新冠肺炎患者置于其他症状之上而导致的，这些附带损害就得不到治疗。

在大流行中，政府和个人采取的措施也会影响死亡率。例如，交通事故的死亡人数可能会下降，但自杀率可能会上升。超额死亡率反映了所有这些因素的净结果。图1说明了新冠肺炎记录相对于过量死亡的程度在一些欧洲国家中是如何变化的。在比利时，对新冠肺炎死亡的定义很宽泛，超过100%的超额死亡可能表明，大多数多出的死亡是由于新冠肺炎，而其他死亡人数，如交通事故，可能已经下降。

超额死亡率数据可以用来从国家间和国家内部的差异中吸取教训，并帮助分析大流行病和放松封锁限制的社会和经济后果。

对于国家比较(记录不足的国家可能有所不同)，政策制定者应该检查相对于“正常”死亡基准所表达的强有力的措施。“正常”死亡率反映了持续存在的因素，如人口的年龄构成、吸烟和空气污染的发生率、肥胖、贫困和不平等的盛行，以及医疗服务提供的正常质量。估计病毒繁殖率R对于评估封锁放松的速度和性质至关重要。1超额死亡数字有助于避免流行病学模型中通常用于估计R的其他数据所固有的测量偏差。2个。

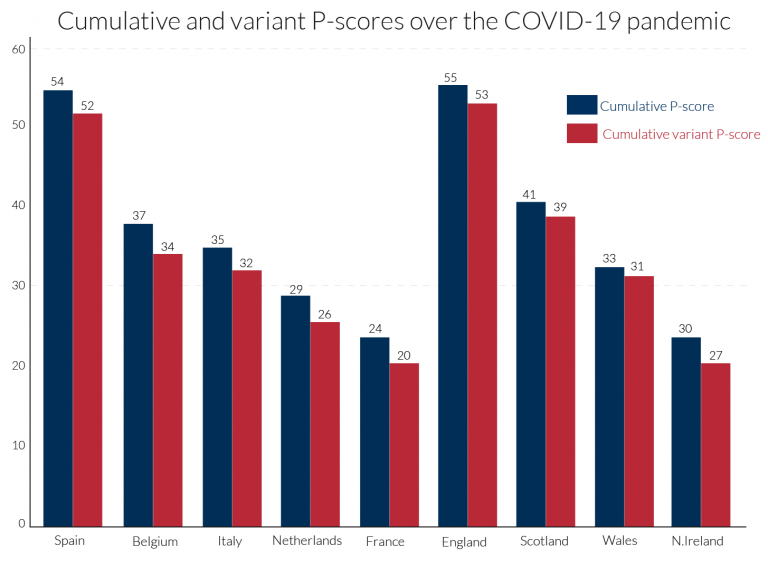
图1：COVID总死亡人数占表现不佳者额外死亡人数的百分比(“所有年龄段”)：在大流行3周内累计。

国家统计机构公布每周实际死亡人数和过去“正常”死亡人数的平均值。例如，英国国家统计局(ONS)报告称，英格兰和威尔士的“正常”死亡人数是前五年死亡人数的平均值。然而，目前还没有公布更细粒度或分类数据的基准，如分区域或城市。使用每周的历史数据，研究人员可以通过一些努力来计算这样的基准。相对于“正常”死亡的超额死亡的比率或百分比，P分数，是一个容易理解的超额死亡率的衡量标准，见方框1。我们认为国家统计局应该公布各州和次区域的P分数。在美国，美国国家卫生统计中心(National Centre For Health Statistics)发布了超额死亡数据和P-Score的变体(见方框1)，将超额死亡定义为偏离“正常”死亡人数，加上根据数据的不确定性进行调整的边际。4这些数据包括县和州，并按性别、年龄和种族分列。因此，NCHS为统计机构制定了一个国际标准。

然而，要获得跨欧洲的比较，需要来自各个国家机构的数据整理，以构建在很大程度上具有可比性的P-分数或变体P-分数，见4.1节。另一种选择是EuroMOMO 5为24个州编制的Z分数，见方框1。EuroMOMO对欧洲每周超额死亡率的测量显示了不同时间段、不同国家和不同年龄组之间的死亡率模式。Z-SCORE以死亡标准差为标度，对超额死亡数据进行标准化处理。欧洲气象组织目前不允许按国家公布实际的超额死亡数字，也不公布计算中使用的标准偏差。然而，他们将Z得分和2015年的估计置信区间绘制成图表，为它们的可变性提供了直观的指南。与P分数相比，Z分数是一种不太容易解释的衡量标准。此外，如果每周数据的自然变异性在一个国家比另一个国家低，那么Z得分可能会导致与P得分相比夸大超额死亡率。严格地说，Z分数在不同国家之间是不可比较的，尽管参见4.1节中的警告。

最近，至少有5家独立的新闻机构参与了耗时的努力，整理和呈现更透明的超额死亡数据，参见表1。英国“金融时报”绘制了超额死亡人数，以及高于正常死亡人数的P分或百分比。“经济学人”展示了前几年的数字和图表。

比较不同地区或国家之间的超额死亡率有几个原因。第一个很简单，就是比较第一波大流行的死亡人数。综合指标很有用，例如相对于正常死亡的超额死亡人数、P得分和相对于人口规模的超额死亡人数，见方框1。这些衡量标准中的最后一个指标有一个问题，即老年人口的正常死亡人数往往较高。这一超额死亡的衡量标准将夸大与年轻人群相比在老年人群中大流行的发病率。第二个原因是，要评估政策回应的效果，需要更深入地挖掘，即使是上述简单的措施也需要进一步解读。各国可能在最初传染源的大小、年龄结构、人口共病分布以及密集城市中心的流行方面有所不同，从而使一些国家更加脆弱。比较年龄标准化死亡率有助于控制年龄结构的差异。最后，比较的第三个动机是一个纯粹客观的动机，那就是提高对感染传播动态、发病率和感染者死亡率的科学理解。这最后一项努力的关键是按年龄、性别、区域以及在可能的情况下按社会经济类别对超额死亡数据进行分类。

最近在英国统计学家之间的一场争论强化了我们论文的观点，那就是现在可以通过聚合和更细粒度的P-SCORE数据来进行超额死亡率的国际可比性。已经有关于不平等和城市密度等相关方面的广泛可用的细粒度数据集，这些数据集可以与这些数据结合起来，说明各国之间的比较，并揭示不同类型政策的有效性。理想情况下，应该有透明的数据定义和各国之间定义的可比性，这可能涉及现有国际机构在数据传播标准方面的协调。这将随着时间的推移而演变，但不排除现在进行分析。重要的是所有人，特别是流行病学、经济学和社会学领域的建模人员都可以获得数据。现在需要具有适当数据的科学分析来为政策提供信息，因为不仅每个国家可能会出现连续的大流行浪潮，而且许多后来经历大流行危机的国家有可能在边境开放时重新引发早期国家的感染，而且未来几年可能会出现大流行。

谈到争议，明镜周刊(2020a)在2020年4月30日卫报的一篇文章中就新冠肺炎感染率和死亡率在一些国家的数据定义差异和数据收集不力提出了有效的观点。我们在这一点上是一致的，但尽管他讨论了关于超额死亡率的更可靠的数据，他认为，我们将不得不等待几个月，如果不是几年的话，我们才能开始在各国之间进行有用的比较。然而，鉴于欧洲的第一波大流行在大多数国家已经接近尾声，现在是进行国际比较的好时机，至少在欧洲内部是这样。事实上，2020年5月4日，三位统计学教授菲利普·布朗(Philip Brown)、詹姆斯·史密斯(James Smith)和亨利·韦恩(Henry Wynn)在一封信9中驳斥了斯皮格哈尔特的说法，称：“是的，各国内部存在不一致、报告不足和异质性，但不同国家采取的政策在效果上显示出非常大的差异，似乎让这种担忧相形见绌。”他们担心的是，这篇文章会转移对政治处理危机的批评(事实上，在他们看来已经这样做了)。他们认为，现在需要结合仔细的建模进行比较，以解释不同地点死亡率和感染率的差异，以改善政策。例如，他们引用了美国的一项模特事业，鲁宾等人。(2020)，其最新版本分析和预测了美国县级的死亡率数据，考虑到了美国各县的当地因素，包括人口密度、吸烟发生率和通过手机移动数据衡量的社会距离。统计学家认为，这样的建模工具适用于国家比较，对于建模测试和追踪到社区层面至关重要。我们在第8节中更广泛地强调了这一模型点。

要解释国家之间超额死亡率的巨大差异，需要考虑几个因素，以及这些因素在国家内部的偏差：前几周的平均感染率，新冠肺炎的平均死亡风险，以及对新冠肺炎特定卫生能力的限制。

转到第一个因素，考虑感染率的差异。比较新冠肺炎平均死亡风险相同的两个国家或地区

最后，应该考虑仅仅超额死亡率统计数字是否足以衡量大流行的影响。卫生经济学文献将质量调整预期寿命(QALY)作为卫生改善政策支出的标准。QALY衡量的是一个人可能预期的合理健康寿命。QALY损失的数量可以补充大流行造成的死亡人数的增加，以此作为衡量其影响的指标。然而，在对QALY损失数量的复杂估计中，需要详细的精算和医疗信息。QALY和QALY的货币价值长期以来一直存在争议，参见Loome和Mackenzie(1989)，但QALY的概念确实关注在大流行中损失的预期年限的相对价值(按年龄组)。正常预期寿命为30岁的劳动适龄成年人的超额死亡率可以与预期寿命为5年的85岁的超额死亡率进行权衡。如果选择更加重视工作年龄成年人的超额死亡率，这将影响不同年龄特定死亡率的国家的比较，见第7节。

4.1我们能否比较各国(各种原因造成的)超额死亡率的不同统计指标？

在人口规模适中的相对同质国家(如欧洲国家、日本和韩国)与中国和美国等大国之间进行比较肯定是困难的，这些国家跨越非常不同的地区，可能会有非常不同的大流行时间和发病率。对于后者来说，将人口稠密的地区或州与规模相当的民族国家进行比较要有意义得多。

P分数、人均超额死亡人数和Z分数在其分子中使用了“正常死亡”的概念，将原始死亡数字与通常预期的数字进行了比较。假设死亡人数的数据定义，如周的定义、收集的死亡人数数据的类型(登记与发生数据，见下文)和收集的及时性在各个国家都是相同的(事实并非如此，见下一小节)，我们考虑第2节中描述的统计指标的相对可比性。对于任何衡量标准，与只检查高峰周相比，很明显，与只检查高峰周相比，累计第一波大流行期间的实际死亡人数和正常死亡人数可以更有力地总结其影响。

不同国家的P得分具有很强的可比性，但需要注意的是，“正常死亡”的衡量标准可能只是一个近似值(见下文)。然而，潜在的死亡人数数据确实需要是透明的和完全可比的，才能使比较有效，见第4.2节。

正常死亡率已经反映了持续存在的因素，例如人口的年龄构成、吸烟和空气污染的发生率、肥胖率、贫困和不平等，以及提供的医疗服务的正常质量。这使得P分特别有吸引力，即使年龄构成和其他持久因素不同。由于他们衡量的是与正常死亡率相比的百分比偏差，这些持续的差异将已经被纳入到“正常”死亡率的定义中。

不同的P分数在正常死亡人数的基础上增加了对历史数据变异性的允许，以定义一个上限(假设是基于正常死亡周围95%的置信区间)。他们定义了相对于该阈值的超额死亡人数，并按相同的阈值进行衡量，以计算百分比。因此，变体P-Score总是略低于简单的P-Score，但会密切跟踪它。因为变种比较复杂，所以简单的P分数更可取。它总是可以伴随着对估计的正常死亡的不确定性边际的指示。当累积数周后，不确定性边际下降，因此简单和可变度量之间的差异更小(参见图3)。

按人口衡量超额死亡人数显然比试图比较人口差异很大的国家的粗略超额死亡人数要好得多。然而，人口老龄化的国家往往会有更高的正常死亡率。这自动意味着，像意大利这样人口老龄化的国家将比英国等人口较年轻的国家拥有更高的人均超额死亡率衡量标准。因此，对人均超额死亡率的比较需要谨慎。支持人均超额死亡率的一个可能的论点是，总人口可以被视为社会吸收超额死亡能力的粗略指标。然而，按照这个逻辑，将多余的死亡人数除以工作年龄人口会更有意义。

正如方框1中所解释的，Z分数通过正常死亡的标准差来降低超额死亡人数。原则上，鉴于泊松分布的假设，见方框1，Z分数不应在不同大小的国家之间进行比较，尽管它们对于比较单个国家的每周超额死亡情况很有用。原因是，与人口较多的国家相比，人口较少、因此每周死亡人数较多的国家相对于正常死亡人数的标准偏差较高。在实践中，由于对泊松分布(见附录1)的不恰当假设，各国之间的超额死亡率排名比预期的更接近P分数。

泊松很可能是死亡人数的随机过程的一个很差的近似值，即使在欧洲气象组织所说的正常季节也是如此。欧洲气象组织将冬季和夏季排除在外，因为流感、恶劣天气或热浪导致的平均死亡人数发生了系统性变化。但假设整个春秋两季的平均死亡人数没有系统性的变化似乎是极端的。如果冬季由于严重的流感导致的死亡人数过多，那么在春季应该会导致低于平均水平的死亡人数。还有其他可能影响死亡率的例子，如麻疹暴发，或改变对无家可归者或疗养院的支持(例如，财政紧缩措施)。在最脆弱的年龄段中，也可能存在不同影响的随时间变化的集群-例如以前接触过不同的风险，如吸烟。因此，恒定均值假设几乎肯定是错误的。关于EuroMOMO用来压低Z得分的“正常”季节的每周标准偏差(见方框1)，测量中将包括系统因素的变化，如那些改变平均值的因素，以及随机噪声(见方框2)。因此，Z分数在分母和分子中包含了这些系统特征。矛盾的是，这使得Z-SCORE有点不稳定。

..