基于网络的新冠肺炎感染曲线多为线性的解释

由挪威奥斯陆大学Nils C.Stenseth编辑，并于2020年7月23日获得批准(2020年5月22日收到供审查)。

很多国家已经度过了新冠肺炎疫情的第一个高峰期。传统的流行病学模型将其描述为非药物干预推动增长率低于恢复率的结果。在大流行的这一阶段，许多国家的确诊病例在较长时间内几乎呈线性增长。这种新的遏制机制很难用传统模型来解释，传统模型要么感染人数爆炸性增长，直到达到群体免疫力，要么疫情完全被抑制。在这里，我们根据联系网络的结构来解释这一令人费解的观察结果。我们证明，对于任何给定的传播率，都存在一个临界的社会接触数Dc，低于这个临界值，一定会出现线性增长和低感染率。在DC以上，发生了传统的流行病学动态，例如，在易感-感染-康复(SIR)模型中。当将我们的模型校准为传播率和传染天数的经验估计时，我们发现Dc∼为7.2.。假设现实的接触网络的度数约为5，并假设封锁措施会将其减少到家庭规模(约2.5)，我们以惊人的精度再现了实际的感染曲线，而不需要拟合或微调参数。特别是，我们比较了美国和奥地利，作为一个最初没有实施措施的国家和一个很早就以严格封锁作为回应的国家的例子。我们的发现对描述新冠肺炎围堵阶段的标准隔室模型的适用性提出了质疑。在这些区域中观察到线性增长的概率几乎为零。

教科书上的流行病学知识说，当人群中的群体免疫力达到(1，2)时，流行病事件就会停止。群体免疫水平取决于疾病。流感的发病率在33%至44%的人口范围内(3例)，埃博拉病毒的发病率为33%至60%(4例)，麻疹的发病率为92%至95%(5例)，报告的严重急性呼吸综合征(SARS)水平在50%至80%之间(6例)。对于目前的新冠肺炎疫情，预计将在29%至74%(7，8)之间。教科书上的知识告诉我们，在获得群体免疫的过程中，只要有效繁殖数量大于1，感染人数的增长速度就会超过线性(在早期甚至是指数级)。一旦超过这个阈值，感染人数的日增量就会开始减少，直到降到零(1，9)。将这两个生长阶段结合起来，得到了特征性的S型感染曲线。

然而，新冠肺炎的爆发展示了一幅非常不同的图景。几个国家显然已经过了疫情的第一个高峰，并且正在向每天零新增病例汇聚。这些国家中没有一个接近于群体免疫力。到目前为止，在奥地利大流行的第一个高峰期，一项具有代表性的全人群PCR研究显示，只有大约0.3%的人口检测呈阳性(10)。同样，在冰岛的随机人群筛查中，阳性检测的流行率被发现为0.8%(11例)。显然，目前新冠肺炎疫情远不是失控病例，因为许多国家已经实施了非药物干预措施来降低感染率(12)。

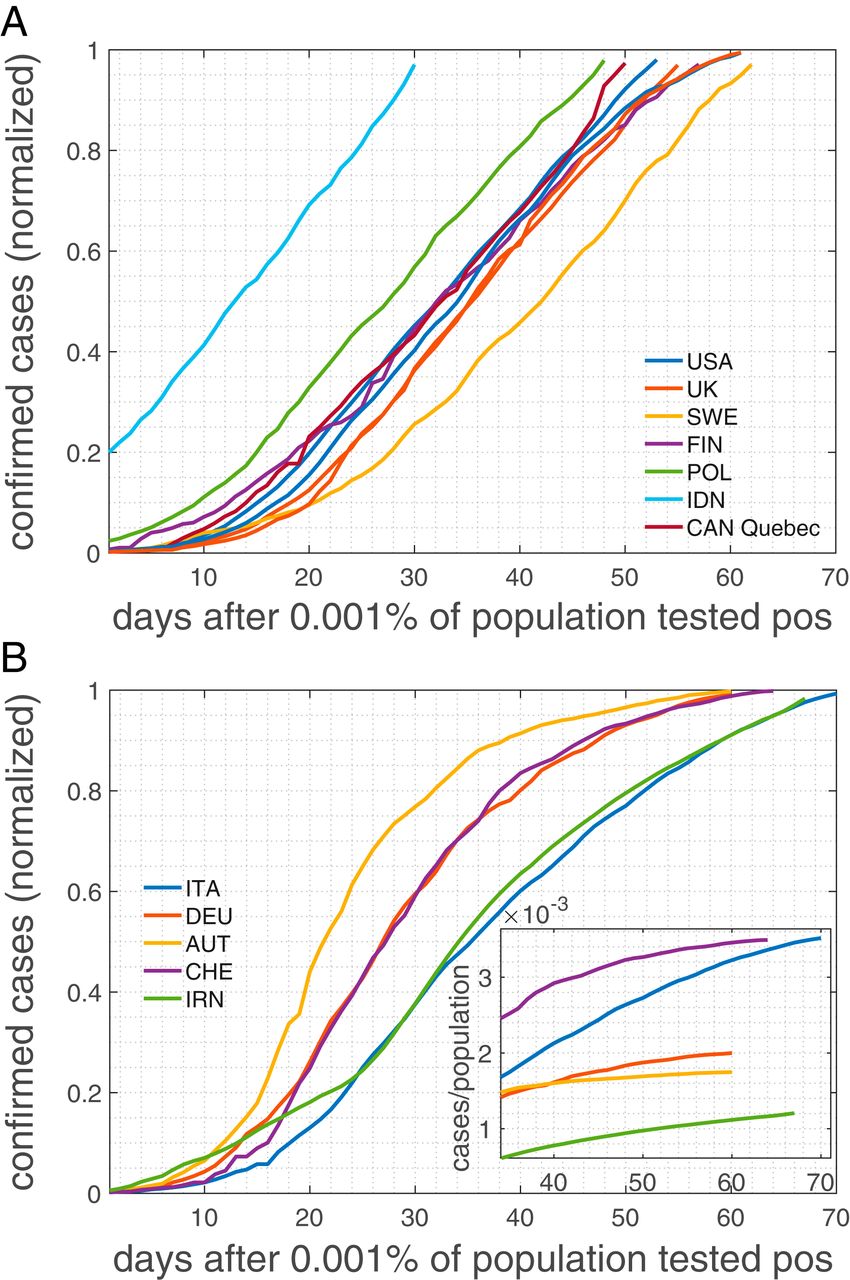
也许在新冠肺炎感染曲线中最引人注目的观察是，它们在较长的时间间隔内呈现线性增长，与流行病学模型预期的S型曲线形成鲜明对比。对于不分大小、人口和种族构成或地理位置的大范围国家而言，即使通过对阳性病例数量(例如REF)的简单检查，这种线性增长模式也是显而易见的。13.在图1A中，我们显示了美国、英国、瑞典、芬兰、波兰、印度尼西亚和加拿大某省的感染曲线(确认阳性病例数)。显然，在短暂的初始指数阶段之后，感染曲线在几周内几乎是线性的。有关其他许多示例，请参见REF。13.为应对新冠肺炎危机而实施的许多国家(12)表现出不同的模式。它们也显示出延长的线性增长；然而，感染曲线往往会随着实施的措施而弯曲和趋于平稳(图1B)。线性制度的程度取决于措施(12)的开始。许多仍处于大流行早期阶段(2020年5月8日)的国家显示出最初几乎呈指数级增长(SI附录，图1)。根据流行病学的基本概念，线性区域延伸的增长模式是不可取的。只有当感染增长率等于恢复率，给出有效繁殖数R(T)为1时，才能观察到它们。观察到这种行为的机会

既然社交网络是了解疫情爆发细节的关键，那么它们是什么样子的呢？答案非常重要，因为社交网络很难定义。在网络拓扑方面，很明显，它们既不是纯随机图，也不是小世界网络，也不是纯粹的无标度网络。它们的结构更为复杂，包括多层次组织(18个)；社区之间的联系薄弱(19个)；以及时间方面，显示出一定程度的流动性，但具有稳定的社会核心(20个)。

在这里，我们试图理解感染曲线中扩展的线性区域的起源，就像目前在许多国家观察到的新冠肺炎大流行阳性检测病例的数量一样。为此，我们在一个简单的社会网络上求解了SIR模型，并报告了一个迄今未观察到的从线性增长到S型感染曲线的转变。我们表明，对于给定的传输速率，存在一个临界度，低于该临界度线性增长，高于该临界度，该模型再现了经典的SIR结果。低于临界度，平均场近似开始失效。对于潜在的社会网络，我们使用泊松小世界网络，该网络试图捕捉几个经验事实，包括不同数量的社会联系(度)、小世界方面、人们倾向于生活在小群体(家庭)中、这些群体重叠以及工作和休闲关系可以将遥远的群体联系起来(方法)。该框架允许我们将锁定建模为高度社交网络向具有家庭成员特征程度的社交网络的转变。基于欧盟家庭规模的数据(21)，基于对个人传染性持续时间的经验估计，以及基于传播(或攻击)率，我们能够将该模型校准到真实国家。特别是，我们比较了美国和奥地利的情况。这些国家在大小和为应对新冠肺炎大流行而采取的措施上存在显著差异(12)。虽然奥地利相对较早地结合其他一些措施实施了封锁，但正如特朗普政府的顾问A·福奇博士在2020年5月12日(22日)所说的那样，美国在实施措施时犹豫不决，结果是局势“没有得到控制”。该模型在很大程度上再现了真实的感染曲线。所有参数都是经验激励的；没有涉及拟合的参数。

我们假设有N个人通过社会关系联系在一起。如果i和j是连通的，则Ai，j=1；如果它们不是连通的，则Ai，j=0。作为社会网络的玩具模型，我们使用了具有平均度D和最短概率ϵ(方法)的所谓小世界网络。小世界方面允许我们对当地群体和“超级传播者”之间的传播进行建模(23)。就像在SIR模型中一样，每个人都处于三种可能的状态之一：易感(S)、感染(I)和康复(R)。如果个人被感染，该个体将以每天的传播概率r感染易感邻居。这意味着在每一天，将感染传染给易感邻居的概率是r，这有时被称为微观传播率(17)。一旦一个人被感染，这个人就会连续d天保持传染性。在此之后，该人不能再感染他人，称为痊愈。一旦恢复，状态将不再改变。相应模型的更新规则为：将所有节点初始化为敏感节点；随机选择N i n i节点，将其状态更改为已感染。在每个时间步t，找到所有被感染的节点，并以概率r感染它们的易受感染的邻居。将所有被感染超过d个时间步的被感染节点设置为恢复。并继续到下一个时间步，直到动力学停止。所有节点现在要么已恢复，要么易受影响。

在每个时间步(天)t，我们计算新病例数C(T)；阳性病例感染曲线P(T)是C(T)的累加和。模型参数与SIR模型(SI附录)的参数相关，γ=1/d，β=rD/N。如果底层网络满足平均场近似所必需的条件，则C(T)对应于R(T)直到d的时移。

我们在图2A-C中对该模型进行了示意性论证，在大D阶和大ϵ的限制下，该模型应该近似满足平均场条件，并且应该接近经典的SIR模型。这在图2D中可以看到，其中对于具有1,000个节点的网络，示出了感染曲线P(T)的轨迹(蓝点)，其程度为D=8，ϵ=0.1，传染性周期d=6d，传播率r=0.1；10个节点在开始时被感染。这种情况与解决方案非常相似。

我们检验了临界度在网络规模和拓扑变化下的位置是相对稳健的。我们发现，对于N=1,000和10的初始感染，临界度实际上在相同的位置。在拓扑结构上，我们实现了一个标准的定度小世界网络。同样在这里，结果实际上是相同的(SI附录，图3)。

对于泊松小世界网络，我们可以用“熔丝模型”Dc∼1+2/(rd(1+ϵ))来解析估计其临界度。[1]有关推导，请参见SI附录，正文S6。这个结果稍微高估了模拟结果(表1)。但是，当r和ϵ较大时，理论预测与模拟结果吻合较好。实际上，所使用的二阶近似系统地低估了传播速度，即高估了网络活动区域中的感染人数，这反过来又导致了对Dc的高估(SI附录，正文S6)。此外，模拟中的有限尺寸效应可能会增加观察到的偏差。

临界度的存在标志着在线性和S形增长之间存在迄今被忽视的转变，这最有可能是由于良好混合或平均场假设在Dc以下崩溃的事实。为了说明这种转变对传输率的依赖性，图3B显示了D=10的网络在r=0.1(红色)的速率下模型感染曲线的20种实现。在选择10个初始感染节点时，得到了20种不同初始条件下的曲线。观察到典型的S型曲线，达到约75%的群体免疫力。值得注意的是，SIR模型的R(t→∞)达到80%左右。对于r=0.05远低于临界度的传输速率较低的同一网络，我们处于线性增长域(绿松石)。最高感染水平仅为1%~4%，大大低于R(t→∞)∼)为15%的SIR群体免疫水平。20条黑色感染曲线描绘了一种“锁定”场景：我们从r=0.1(红色)的相同网络开始。在5%的人口被感染的那一天(黑条)，就会实施封锁，这意味着社交网络实际上每天都在发生变化。我们通过切换到一个低度的泊松小世界网络(D2=3)来对此进行建模，所有其他参数保持不变。S型生长停止，最终感染水平约为10%。

通过在从公开可用的实际联系网络(26)导出的网络上运行该算法，我们确认对于更现实的社会联系网络(20、24、25)也存在获得线性感染曲线的机制。对于这些网络的度低于Dc的情况，我们通常观察到线性感染曲线。详细信息见图7的SI附录。

我们对美国和奥地利两个国家的新冠肺炎感染曲线进行了校准，以证明该模型在估计非营利组织感染效应方面的潜在适用性。为此，我们必须对模型参数作出以下假设：

新冠肺炎的病毒动力学是高度异质性的(27)。有证据表明人们携带病毒载量，因此可以在发病后20多天内具有传染性(大多数人的传染性时间较短)(28，29)，考虑到传染性可以在出现症状之前2到3天开始(28)，我们使用d=14 d。

2019年，欧盟的平均家庭规模为2.3人(21人)。如果我们假设，在工作和休闲活动中，人们平均每天多会见3到4个人，我们决定在正常情况下，在我们的泊松小世界中使用D=5的平均度数。如果我们假设平均约有30%的社会关系在我们的家庭之外，我们将ϵ设置为0.3。这是一个有点武断的选择；然而，请注意，在线性机制的深处，ϵ被发现是一个几乎不相关的参数，不会以显著的方式影响结果。为了将2020年3月16日在奥地利实施的封锁模拟为NPI，我们假设其效果基本上是将社交联系减少到家庭内部，并消除任何其他联系。对于此场景，我们假设D=2.5，ϵ=0。最后，对于每天的传输速率，我们设置r=0.0149。这一选择的动机是估计新冠肺炎在家庭环境中的个人水平二次发作率，据报道约为19%(30)，关系r=1−(1−S A R)1/d。请注意，这些参数的估计是基于最近的估计(尚未进行同行评审)，未来可能会发生变化。还请注意SIR限制。

.