将模糊不清的有限状态机转换为正则表达式

我喜欢一个Twitter帐户@happyautomata，该帐户会定期发布随机生成的有限状态机。该帐户的追随者倾向于将FSM转换为正则表达式。这始终是可能的，因为（严格地是正则表达式）正则表达式和有限状态机彼此完全等效。有时，这很容易，您可以在脑海中做到。

但是有时候这是非常棘手的，您必须手工解决。但是如何？

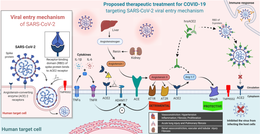
请注意，我已经在状态机中的四个状态（A，B，C和D）中添加了标签。初始状态为A。每个状态都转换为其他状态。例如，

从状态A开始，如果机器消耗了🌹，那么我们跳到状态B。

从状态B开始，如果机器消耗了🌵，则我们再次跳至状态B。

此外，带有两个圆圈的状态是最终状态。在消耗完所有输入后，如果我们处于状态B或状态D，则机器接受输入。例如，本机接受字符串＆＃34;🌹🌼🌼＆＃34 ;，但不接受＆＃34;🌹🌼🌳＆＃34;。如果缺少转换，则机器绝对不会接受该字符串。因此，＆＃34;🌵🌵🌵＆＃34;不被接受；如果这样做的话，我们就会掉出机器。

我们可以用一组联立方程的形式来表示所有这些。

A =🌱A | 🌹B | 🌲C | 🌵D B =ε| 🌵B | 🌼C C =🌳C | 🌼D D =ε

A，B，C和D不是数字，它们是字符串集。例如，如果我们从A＆＃34;开始，则A表示＆＃34;可接受的字符串集。

诸如＆＃34;🌹B＆＃34;之类的表达式也是一组字符串：它表示＆＃34;取B中的每个字符串并在前面加put时得到的组。类似于＆＃34;的表达式C =🌼D＆＃34;表示＆＃34; C中的每个字符串c对于D＆＃34;中的某些字符串d都具有🌼d的形式。

ε表示空字符串。例如，由于B和D是最终状态，因此空字符串是它们接受的字符串之一。

我们需要解决A。让我们从头开始。这种技术称为Brzozowski代数方法。首先，将D的方程式替换为所有较早的方程式，将其消除：

A =🌱A | 🌹B | 🌲C | 🌵B =ε| 🌵B | 🌼C C =🌳C | 🌼

现在，让我们看一下C的等式。请注意，C具有自变迁🌳。这意味着我们可以输入🌳零次或多次，然后返回C。自我转换非常重要，必须首先处理。我们可以使用Kleene星来做到这一点：

A =🌱A | 🌹B | 🌲C | 🌵B =ε| 🌵B | 🌼C C =🌳*🌼 然后，我们也可以将C的等式代入所有先前的等式中： A =🌱A | 🌹B | 🌲🌳*🌼| 🌵B =ε| 🌵B | 🌼🌳*🌼 注意，在A和B的方程式中，我们有两个＆＃34; static＆＃34; 术语-纯正则表达式，不引用其他状态。 让我们将它们组合在一起。 注意我们如何使用正则表达式语法中的问号元字符，这意味着＆＃34; this或空字符串＆＃34 ;： A =🌱A | 🌹B | 🌲🌳*🌼|🌵B =🌵B | （🌼🌳*🌼）？ 现在让我们看一下B的方程式。它也具有自变迁。 因此，让我们现在解决这个问题。 （在此之前，我们无法解决。） A =🌱A | 🌹B | 🌲🌳*🌼|🌵B =🌵*（🌼🌳*🌼）？

A =🌱A | 🌹🌵*（🌼🌳*🌼）？|🌲🌳*🌼|🌵

A =🌱*（🌹🌵*（🌼🌳*🌼）？|🌲🌳*🌼|🌵）

我们完成了！我们有一个A的正则表达式。这是一个严格的正则表达式。它没有高级语法，例如反向引用或环顾断言（并非严格规则），并且隐式地锚定在输入字符串的开头和结尾。这是正确的答案。

好吧，这是许多可能的正确答案之一。通常有很多方法可以将任何特定的有限状态机表示为正则表达式。您可以在上方看到我们可以选择其他方式来简化表达。尽管我们必须以A结尾，但我们不必以D开始替代。

此外，找出许多等效正则表达式中最小的正则表达式在计算上也非常困难。

通常，即使使用正则表达式标准，有限状态机的正则表达式也可能非常复杂且难以阅读。

不久前，我创建了一个名为greenery的Python程序包，该程序包除其他功能外，还旨在将有限状态机转换为正则表达式。您要做的就是确保手动正确设置状态机及其所有转换，因为状态机无法直观地解析和解释那里的令人愉悦的图像：

从绿色植物进口的fsm，乐高 植物= fsm.fsm（ 字母= {＆＃34;🌱＆＃34;，＆＃34;🌹＆＃34;，＆＃34;🌵＆＃34;，＆＃34;🌲＆＃34;，＆＃34;🌳＆＃ 34 ;,＆＃34;🌼＆＃34;}， 状态= {＆＃34; A＆＃34;，＆＃34; B＆＃34;，＆＃34; C＆＃34;，＆＃34; D＆＃34;}， 首字母=＆＃34; A＆＃34 ;， 决赛= {＆＃34; B＆＃34 ;,＆＃34; D＆＃34;}， 地图= { ＆＃34; A＆＃34 ;： {＆＃34;🌱＆＃34 ;：＆＃34; A＆＃34 ;、＆＃34;🌹＆＃34 ;：＆＃34; B＆＃34 ;、＆＃ 34;🌲＆＃34 ;：＆＃34; C＆＃34 ;，＆＃34;🌵＆＃34 ;：＆＃34; D＆＃34; }， ＆＃34; B＆＃34 ;： {＆＃34;🌵＆＃34 ;:＆＃34; B＆＃34 ;,＆＃34;🌼＆＃34 ;:＆＃34; C＆＃34; }， ＆＃34; C＆＃34 ;： {＆＃34;🌳＆＃34 ;:＆＃34; C＆＃34 ;,＆＃34;🌼＆＃34 ;:＆＃34; D＆＃34; } } ） compute_regex = lego.from_fsm（植物） 打印（compute_regex）

🌱*（（🌲|🌹🌵*🌼）🌳*🌼|🌵|🌹🌵*）

🌱*（🌹🌵*（🌼🌳*🌼）？|🌲🌳*🌼|🌵）

它们看起来大致相等，尽管尚不清楚它们实际上是否相等。有办法确定吗？狡猾，有！ greenery还提供了一个API，用于确定两个正则表达式是否等效：

handmade_regex = lego.parse（＆＃34;🌱*（🌹🌵*（🌼🌳*🌼）？|🌲🌳*🌼|🌵）＆＃34;） 打印（compute_regex.equivalent（handmade_regex））

这相当复杂，因为当状态B消耗a时，它同时转换为状态C和状态D。

实际上，这是在引入一种新的＆＃34; compound＆＃34;状态机同时处于C和D的状态。我们将此新状态称为C + D。 C + D跃迁只是C和D跃迁的总和...但是随着我们的不断发展，我们发现越来越多的复合态。

这种事情可能会变得非常复杂。从理论上讲，对于具有N个状态和这种多转换的有限状态机，最多可以有2 N-1个可能的化合物。状态。在这种情况下，转换后的4个州可能意味着多达15个复合状态。

我们还必须记住，如果复合状态的任何子状态都是最终状态，则该复合状态本身就是最终状态。例如，此有限状态机接受两个字符的字符串＆＃34;🤍💙＆＃34 ;，使其处于状态C + D，因此是最终状态。

心= fsm.fsm（ 字母= {＆＃34;🤍＆＃34;，＆＃34;💙＆＃34;，＆＃34;❤️＆＃34;}， 状态= {＆＃34; A＆＃34;，＆＃34; B＆＃34;，＆＃34; C＆＃34;，＆＃34; D＆＃34;，＆＃34; C + D＆＃34 ;、 ＆＃34; A + D＆＃34;，＆＃34; A + C＆＃34;}， 首字母=＆＃34; A＆＃34 ;， 决赛= {＆＃34; B＆＃34;，＆＃34; D＆＃34;，＆＃34; C + D＆＃34;，＆＃34; A + D＆＃34;，＆＃34; A + B＆ ＃34;}， 地图= { ＆＃34; A＆＃34 ;： {＆＃34;🤍＆＃34 ;:＆＃34; B＆＃34 ;,＆＃34;💙＆＃34 ;:＆＃34; C＆＃34;}， ＆＃34; B＆＃34 ;： {＆＃34;💙＆＃34 ;：＆＃34; C + D＆＃34 ;，＆＃34;❤️＆＃34 ;：＆＃34; B＆＃34;} ， ＆＃34; C＆＃34 ;： {＆＃34;🤍＆＃34 ;:＆＃34; A＆＃34 ;,＆＃34;💙＆＃34 ;:＆＃34; D＆＃34;}， ＆＃34; D＆＃34 ;： {＆＃34;💙＆＃34 ;：＆＃34; A＆＃34;}， ＆＃34; C + D＆＃34 ;： {＆＃34;🤍＆＃34 ;：＆＃34; A＆＃34 ;、＆＃34;💙＆＃34 ;：＆＃34; A + D＆＃34 ;}， ＆＃34; A + D＆＃34 ;： {＆＃34;🤍＆＃34 ;：＆＃34; B＆＃34 ;、＆＃34;💙＆＃34 ;：＆＃34; A + C＆＃34 ;}， ＆＃34; A + C＆＃34 ;： {＆＃34;🤍＆＃34 ;：＆＃34; A + B＆＃34 ;、＆＃34;💙＆＃34 ;：＆＃34; C + D＆ ＃34;}， ＆＃34; A + B＆＃34 ;： {＆＃34;🤍＆＃34 ;：＆＃34; B＆＃34 ;、＆＃34;💙＆＃34 ;：＆＃34; C + D＆＃34 ;，＆＃34;❤️＆＃34 ;:＆＃34; B＆＃34;}， } ） compute_regex = lego.from_fsm（hearts） 打印（compute_regex）

（💙（💙{2} |🤍）|🤍（❤️|💙（💙{2}🤍？💙）*💙（💙🤍[❤️🤍] |🤍））*💙（💙{2}🤍？💙）* 🤍）*（💙{2} |🤍（❤️|💙（💙{2}🤍？💙）*💙（💙🤍[❤️🤍] |🤍））*（💙（💙{2}🤍？💙）*（ 💙（💙🤍）？）？）？）

那用手呢？好吧，这个方法看起来很讨厌手工处理，但这是一个同样可怕的提议解决方案，它可能是手工计算的，也可能不是。通过视觉检查猜测这些是否相等可能是徒劳的。因此，让我们使用Python看看...

handmade_regex = lego.parse（＆＃34;（💙（🤍|💙💙）|🤍（❤️|💙（💙💙🤍？💙）*💙（🤍|💙🤍（🤍|❤️）））*💙🤍）* （💙💙|🤍（❤️|💙（💙💙🤍？💙）*💙（🤍|💙🤍（🤍|❤️）））*（💙（💙💙🤍？💙）*（💙（💙🤍）？）？ ）？）＆＃34;） 打印（compute_regex.equivalent（handmade_regex））

这表明存在分歧。如何找出可能的差异？好吧，首先我们可以将这两个正则表达式的对称差计算为一个新的正则表达式（实际上，.equivalent在内部是这样工作的），然后可以迭代这个新的正则表达式的字符串：

是的，我们可以在这里看到字符串＆＃34;🤍💙💙💙💙🤍🤍＆＃34;被计算的正则表达式（以及原始状态机）接受，但是，如果仔细观察，则不会被手工表达式接受。

总而言之，我发现所有这些都非常令人愉快和有趣，我希望您也能做到。

我突然想起这是我最初从QNTM那里学到的正则表达式。 嗯 时间飞逝。

既然已经在Code中添加了它，Sam终于完成了将新条目添加到站点的每个部分！

我走得比想像的要多得多，我想检查一下计算的和手工的正则表达式，看看它们有多相似。直到💙{2}（与corresponding对应）相同，并且管道表达式的排序顺序不同，其中很多是相同的。

我认为在第二个示例中合并状态实际上并不是必需的，因为正则表达式是不确定的。您应该只能将其保留为B =❤️B| 💙C| 💙D| ε。 无论如何，我得到了（♡❤️*💙（💙💙？|♡）|💙（💙💙|♡））*（♡❤️*（💙？💙？）|💙💙）