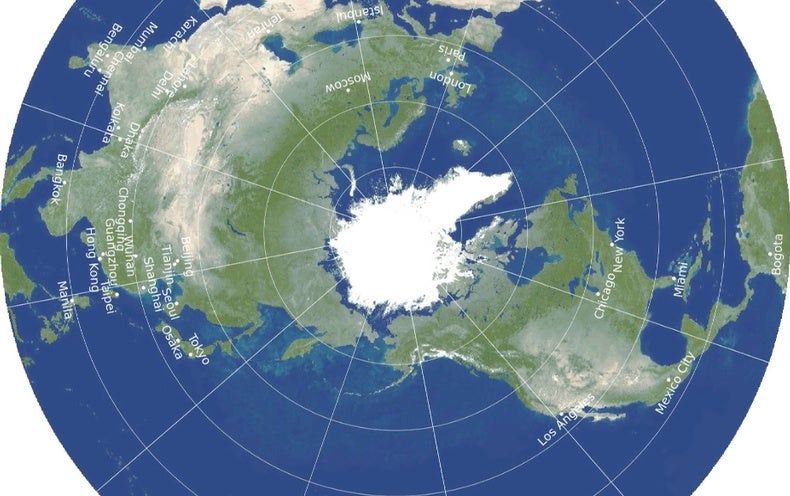
地球上最精确的平面图

我通常从事广义相对论和宇宙学的研究。我一直喜欢几何的东西。小时候，我对地图投影着迷。 14岁那年，我根据天文学家E. M. Antoniadi的墨卡托（Mercator）火星平面图制作了火星地球。自从在普林斯顿大学（Princeton）担任名誉教授以来，我很喜欢回到我的童年时代。

我和我的同事戴夫·戈德伯格和鲍勃·范德贝（他们发明了“紫色美国”地图来显示选举结果）制作了我们认为是迄今为止最精确的地球平面图。几个世纪以来，在平面地图上描绘地球的弯曲表面一直是制图师的难题。没有平坦的地球地图可以完美。但是平面地图易于存储和制造，因此是可取的。

以前，Goldberg和我确定了平面图可能具有的六个关键错误类型：局部形状，区域，距离，弯曲（弯曲），偏斜（偏斜）和边界切割。著名的Mercator投影（谷歌地图的基本模板）对此进行了说明。它具有完美的局部形状，但很难描绘区域。格陵兰岛的面积与南美一样大，尽管它仅占全球面积的七分之一。

不能使所有事情都完美。墨卡托（Mercator）地图存在边界切割错误：沿着国际日期线的子午线从极点到极点切开180度，并展开地球表面，因此将夏威夷置于地图的最左侧，将日本置于地图的最左侧地图的最右侧会在此过程中造成额外的距离误差。一名飞行员从纽约直飞东京，沿大圆环路线飞过阿拉斯加北部。他的路线在墨卡托（Mercator）地图上看起来弯曲-弯曲错误。北美偏北：加拿大比其应有的更大，而墨西哥却太小。所有这些错误都很重要。忽略其中之一可能会导致您看到任何人都不喜欢的外观不好的地图。

这里的目的是找到最小化误差平方和的地图投影，这项技术可以追溯到数学家卡尔·弗里德里希·高斯。墨卡托投影的Goldberg-Gott误差得分（六个标准化的单个误差项的平方和）为8.296。分数越低，错误越小，地图越好。地球地球仪的错误分数为0.0。我们发现，对于地球而言，最著名的平面投影是美国国家地理学会使用的Winkeltripel，其错误评分为4.563。它的顶部和底部具有直的极线，左右边缘凸出，标志着其在太平洋中部的180度边界切割。

我们似乎在改善Winkel三角架上已达到极限。在科学中发生这种情况时，通常需要突破性思维，一些开箱即用的思维才能取得根本性的进步。理查德·费曼（Richard Feynman）曾经说过，在物理学中，当我们陷入困境时，如果所有旧方法都不起作用，那么新的技巧，将要起作用的新方法将与我们之前所见的任何事物都有很大的不同。

新地图投影的想法来自我最近写的一篇论文《信封多面体》，其中介绍了新的一类常规多面体，其中允许多边形连续显示。我意识到我可以制作一张背对背的圆形地图：就像老式留声机唱片一样。地图的一侧显示了北半球，另一侧显示了南半球，赤道围绕边缘运行。它没有边界切割，也没有球体的正确拓扑。一个简单地将球压扁。

然后，我们必须找到用于绘制每侧特征的最佳公式，该公式将使Goldberg-Gott错误分数最小化。答案是这样的：北极出现在留声机唱片北侧的中央，经度线从其均匀分布，从而使每个经度线上的音阶均匀，南端也是如此。城市之间的距离是通过在城市之间简单地拉一条线来测量的。如果它们在相反的半球中，则字符串仅会延伸到地图边缘的赤道。

新地图的一个缺点是您无法一次看到地球的所有表面，但请记住，这对于地球也是一样。在这方面，我们的地图实际上比其他平面地图更像地球。要查看整个地球，您必须旋转它。要查看所有新地图，只需将其翻转，如下所示

这张双面地图的Goldberg-Gott误差得分仅为0.881，而Winkel三角架的得分为4.563。在六个错误方面，它都击败了Winkel tripel！由于大陆和海洋在圆形边缘连续，所以边界切割误差为零。它具有无与伦比的单面平面地图的显着特性：点对之间（例如城市）之间的距离误差是有界的，最多不超过正负22.2％。在墨卡托（Mercator）和温克尔（Winkel）三轴投影中，距离误差会随着接近极点和边界切线而增大。

我们的地图可以从杂志上剪下或插入活页中。它们可以由硬纸板或塑料制成。一个细盒子可以容纳太阳系中所有主要物体的平面双面地图，也可以放置一堆提供物理和政治数据的地球地图。

温克尔三脚架是一张挂在墙上的地图。我们的是您可以拿到的更准确的一种。