贝叶斯定理：批判性思维的框架

你有没有注意到，你是如何在前一秒怒气冲冲，下一秒又完全平静下来的？

一个混蛋司机在高速公路上拦下你，你就大发雷霆了。过了一会儿，你注意到他把车开进了医院，你的怒火就消失了。“是的，也许他车里有个病人。或者，也许亲近的人快要死了。我猜他终究不是个混蛋。“。

概率论中的一条晦涩难懂的法则，叫做贝叶斯定理，很好地解释了这一点。这篇9000字的博客文章完整地介绍了贝叶斯定理以及如何将其付诸实践。简而言之，贝叶斯定理是批判性思维的框架。在这篇文章的最后，你会做出更好的决定，意识到你什么时候是不讲理的，也明白为什么有些人相信不明飞行物。

这是一个巨大的承诺，失败的可能性很大。实施这些想法需要情感上的努力，但这是值得的。

认为司机是个混蛋是很正常的。贝叶斯定理也期待着同样的结果。贝叶斯和我们的不同之处在于我们相信的强度。大多数情况下，怒火冲天是没有根据的。这可能就是为什么我们对所有的愤怒感到愚蠢的原因。它融化得太快了！这是校准-使我们的情绪与情况的强度保持一致-我们也会讲述这一点。

这本指南中没有花哨的数学知识。我们用的是概率论，但不会去推导，也不会解决课本上的概率问题。在不了解原因的情况下，这些事情是单调乏味的。相反，我们将理解为什么贝叶斯定理很重要，以及如何应用它。

首先，让我们玩个游戏。在整个游戏中，注意你对你的决定的感觉。注意你正在做的决定，注意你是如何找到答案的。

有一个黑匣子，里面有一个生成3个数字的公式。你的工作就是试着猜出这个公式。下面的输入框已连接到黑框。如果你给它3个数字，它会告诉你他们是否遵循公式。用逗号分隔每个数字。

大多数人尝试一些序列：(4，6，8)，(1，2，3)…。结果要么是数字递增，要么是偶数递增。注意当你写下答案的时候，你是如何对自己的答案充满信心的。您已经尝试了几个示例，所有这些示例都很有意义！

如果我的评论让您的信心动摇，请继续并再次尝试输入框。看看你能不能找到一种有效的模式。答案就在这一节的底部，但不要跳过。在此之前的每一句话都是在建立一个重要的思想。

事实上，这就是问题的全部。我打赌你也听说过这个著名的公式：\(e=mc^2\)。这就是质能等价性的全部内容。然而，弄清楚如何利用核能仍然是一个难题。这个公式使之成为可能，但实施它仍然花了40年的时间。

这与贝叶斯定理是一样的。这个公式之所以令人兴奋，是因为它暗示了什么。我们正在发现核能版的贝叶斯定理。

为了形成准确的信念，你总是从你已经拥有的信息开始。你更新了信仰。你不会抛弃你所知道的一切。

第一个关键部分是假设(H)--我们正在谈论的信念。

第二个关键部分是证据(E)--我们有什么数据来支持/拒绝这一假设。

第三个关键成分是以上两者的概率(P)。这个概率就是我们对信仰的信心。

如果你熟悉概率论，你会在学校里学到这一点。如果没有，请不要担心，有很好的数学介绍可以为您解释。我们将跳过数学，专注于如何使用它。

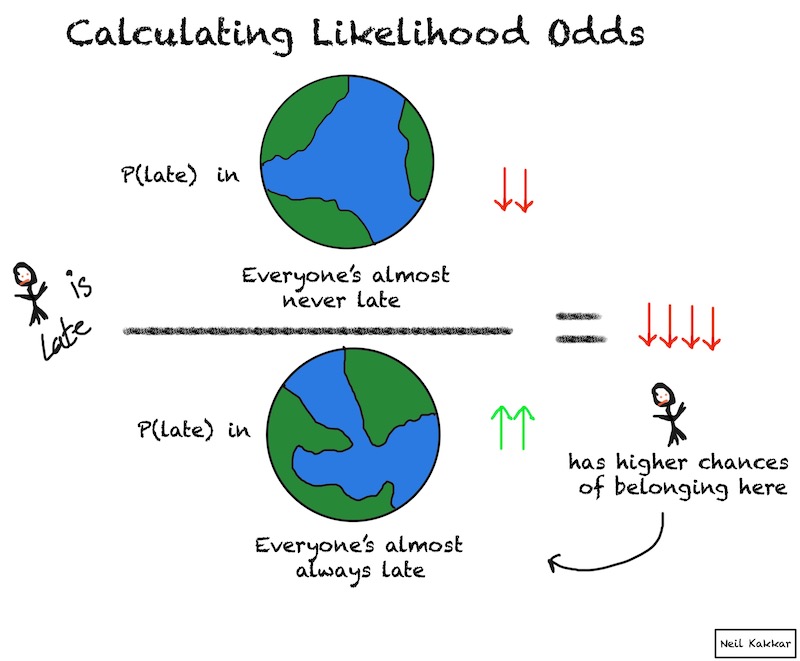
我们的兴趣点，以及贝叶斯真正闪耀的地方，是我们比较两个假设的地方。这不是揭示绝对概率(这很难)，而是关注一种假设与另一种假设相比有多大的可能性。我们头脑中的大多数推理都采用这种形式。

可能性赔率衡量的是，与另一种假设相比，证据对当前假设的解释有多好。我们将借助示例来探索这意味着什么。

假设{hspace{2 mm}假设{hspace{2 mm}为真}{hspace{2 mm}的概率{2 mm}假设\hspace{2 mm}竞争{2 mm}假设\hspace{2 mm}为\hspace{2 mm}假设{hspace{2 mm}证据{2 mm}的可能性{hspace{2 mm}=frac{hspace{2 mm}假设\hspace{2 mm}假设{hspace{2 mm}为真}{hspace{2 mm}假设{hspace{2 mm}为\hspace{2 mm}假设\hspace{2 mm}为\hspace{2 mm}假设{hspace{2 mm}为\hspace{2 mm}假设{hspace{2 mm}为\hspace{2 mm}。

我们将从2，4，6游戏开始，展示数学和直觉在质量上是如何一致的。然后我们将进入一个更简单的例子，在那里我们被错误校准，并进行数学计算。

我将在第2，4，6场比赛中选择我的道路，但我希望你的道路足够相似。如果没有，试着自己做这件事！

我有一个假设要检验，\(H3Even}\)=3个升序的偶数。它在这里是隐含的，但我要测试的假设是\(H_{非-3EVEN}\)，或者公式不是升序的3个偶数。

我输入(4，6，8)，黑框说“是”。我对3个偶数的信心上升了。用贝叶斯的话说，我的后验赔率增加了，因为可能性赔率增加了。当公式为\(H3EVEN}\)时，(4，6，8)说“是”的概率更高，因此可能性几率也增加了。

你会注意到你的感受，每一个与你的假设相匹配的新数字都会让你的信念更加坚定。

接下来我试(1，2，3)。“是的”。什么？我还以为会说“不”呢！

当你发现一些不符合模式的东西时，一切都会像它应该的那样翻滚。由于(1，2，3)不都是偶数，所以(1，2，3)说“是”的概率随着(H_{非-3偶数})的增加而增加。现在可能性赔率偏向\(H_{非-3偶数})，这意味着我们放弃\(H_{3偶数}\)。在这种情况下，一个小小的证据就足以完全颠倒天平。

那么，你应该尝试哪种新的假设呢？线索通常在于你如何反驳先前的假设。

我试了(1，2，3)，它说“是”，而我预计它会说“不”。因此，我的新假设变成了“3个递增的数字”。

就像前面的例子一样，(4，2，6)说“是”就否定了这个假设。因此，我的新假设变成了“3个正数”。

我试了(-1，2，3)，结果是“不”！这就是我对“3个正数”变得相当有信心所需要的一切。我尝试的负数越多，我就越自信。

校准是关键。我们刚才展示的是我们的思维过程，以及当我们思考得好的时候，贝叶斯定理是如何与之保持一致的。贝叶斯定理更新信念的方向与我们的大脑相同，但改变的是每一件证据对我们的影响有多大！

在下一个示例中，让我们学习基本的数学知识。稍后我们会重温第2，4，6场比赛。

你的同事有时上班会迟到。在过去的一周里，他们已经准时4次，迟到3次。你还需要多少次才能开始相信他们“总是”迟到？

根据我的经验，再多做几次就行了。但是让我们用贝叶斯来校准。

由于没有很好的理由期望迟到胜过准时，让我们假设先前的赔率是1：1.2。2另一种假设，我们正在测试的假设是“并不总是迟到”。更具体地说，我们假设这意味着他们只有10%的时间迟到。3个。

我们将使用我们拥有的数据来计算迟到的可能性。我们想将迟到三次、准时四次的数据与我们认为的几乎总是准时或几乎总是迟到的数据进行对比。记住，为了弄清楚这一点，我们想象相信第一个假设，然后判断数据的可能性有多大。然后，我们想象相信第二个假设，并判断数据的可能性有多大。

有几种方法可以从数学上表示这些数据，从二项式函数到Beta分布。然而，我们还没有开始讨论这个。今天更多的是关于一个直观的解释，一个你更有可能每天都会用到的解释。所以，试着想象一下，给定这些数据，胜负的几率会有多大。4.。

对于一个本该总是迟到的人来说，他们准时的次数比不准时的次数多，这让我有点惊讶。因此，对于我们的假设来说，这一证据几乎是不可能的，而当他们并不总是迟到时，这一证据就更有说服力了。我估计赔率是1：10.5。

现在，后验概率是\(1：10*1：1=1：10\)。因此，他们迟到的可能性比不迟到的可能性低10倍。

让我们进一步看这个例子。比方说，我们想知道他们还要迟到多少次才能把赔率提高到100：1？

因此，可能性比=100：1/1：10=1000：1。这意味着，他们必须在20天中有12天迟到才能得到这样的赔率。6个。

这些数字可能会让人感觉很奇怪。他们是。我们不习惯校准，在这个特殊的情况下，我们比较了两个极端的假设，这让事情变得更奇怪。通常情况下，这是一个“我不知道这些数字是什么意思”的情况。稍后我们将探讨这种令人不安的感觉。

这两种假设都不再接近我们的预期。毕竟，这位同事20天中只有12天迟到了！？为什么我们不考虑另一种假设-比如说，他们60%的时间都迟到了？尝试这个假设，它应该会把另外两个人赶出公园。你可以用我造的这个计算器。

现在，请注意，一些数学知识可以帮助我们更好地校准我们已有的假设。它把我们的情绪和思想放在正确的角度。

还要注意我们是如何将问题转化为更容易理解的。我们不是应用需要纸和笔的复杂版本(概率是多少，公式是什么，我如何找到它们？)，而是遵循这个“旧的赔率乘以当前的可能性等于新的赔率”。

当你有了这个模型来解释“理想的你”是如何思考的时候，你就会有一个齿轮级的理解！这是史诗般的，因为你可以摆弄齿轮，看看你的思维是如何变化的。您可以找出最佳实践，并成为更强大的思考者。这正是我们下一步要做的。

让我们开始磨这些齿轮吧。本节的一个元目标是使齿轮对您可见。我们正在慢慢地接近核能版的贝叶斯定理，但到目前为止，我们刚刚看到了它是如何实现的。下一步是学习如何自己做这件事。

让我们首先假设他们是贝叶斯的，并遵循规则。他们能得出不同的结论吗？

是!。目前的数据只给了我们可能性赔率。还有第二个组成部分，也就是前科，尚未使用！在“迟到”的例子中，我们用我们的背景知识想出了它们。这就是它们被称为先驱的原因：这是我们已经拥有的信息。

两个不同的人有不同的经历和不同的信息，这似乎是有道理的。也就是说，他们可以有不同的前科。有时候，这些前科可能会变得相当强烈。看到同事7天中有3天迟到的你，与看到同事10天中有6天迟到的鲍勃相比，会有不同的前科。鲍勃看到你的同事迟到的次数是原来的两倍！

比起鲍勃，看到你的同事第二天准时会更多地改变你的信心。你能算出差多少钱吗？

For You=1：20(以前，7天中有3天迟到)*(1：20)=1：400=400倍可能相信他们的同事并不“总是”迟到。

对于Bob=300：1(以前，10天中有6天迟到)*(1：20)=15：1=15倍可能认为他们的同事“总是”迟到。

但是，如果两个人都遵循贝叶斯规则，他们都会朝着相同的方向更新，而且更新的百分比也是相同的-这是由似然比给出的百分比。在这种情况下是(1：20)。再次注意数字感觉有多奇怪，比如，这不应该是正确的。

第二种情况是人们根本没有遵循贝叶斯规则。记住，贝叶斯是处方，不是描述！这意味着事情应该是这样的，而不是现在这样。这就是事情变得不明朗的地方。我们很容易将反对某一信仰的证据编织成支持某一信仰的证据。特别是如果假设不是很清楚的话。我们很快就会进入这个话题--只有几个首先要攻击的点子。

贝叶斯定理已经存在了200年，在这段时间里，人们已经用齿轮进行了试验，以得出最佳实践。多亏了这些人，我们将探索由贝叶斯定理驱动的4个想法。掌握这些是成为更好的思考者的关键。

在这个镜头里，世界是概率的。基于你对世界的了解，任何事情都有发生的可能性。概率是你固有的，而不是物体或情况。

例如，在枪战中发动袭击在你看来可能是不可信的，但黑手党暴徒会不同意。你对世界的了解决定了你的概率。这些概率是你对某一信仰的信心。

你遇到一位数学家，她告诉你她有两个孩子。你问他们中是否至少有一个是男孩。她说可以。然后你决定他们两个都是男孩的概率一定是三分之一。

你会遇到另一位数学家。她告诉你她有两个孩子。你问大一点的是不是男孩。她说可以。然后你决定他们两个都是男孩的概率一定是1/2。

你会遇到另一位数学家。她告诉你她有两个孩子。你问年轻的那个是不是男孩。她说可以。然后你决定他们两个都是男孩的概率一定是1/2。

如果他们中至少有一个是男孩，那么无论是大的还是小的都是男孩。那是怎么回事呢？为什么概率不同呢？如果孩子天生就是男孩，那么答案应该总是一样的。

概率是不同的，因为每个问题告诉你关于这个世界的一些不同的东西。每个问题携带的信息量不同。

注意这个问题是如何以不同于下面的方式切分可能性的。第一个问题只删除了一个可能性GG，而另外两个问题分别删除了两个可能性。7个。

同样的想法也适用于找出你的前科。不同的人得出不同的概率是可以的，因为概率是观察者的函数，而不是对象的属性！概率代表你的信念和信息。太阳没有概率，是你相信它每天都会升起。你相信多少可以随着你活着的天数，或者人类存活并记录太阳的天数，或者如果你相信科学家和他们的方法-数十亿年。当然，如果你住在北极或南极附近，你的前科肯定会不同。太阳的存在并不意味着它每天都会升起。

在第2，4，6个游戏中，当你发现更多支持你的假设的证据时，你的信念会变得更加坚定。这个游戏是残酷的：一次失败，这个假设就结束了。这是该假设的一个性质。你能查出是什么房产吗？我们很快就会讲到的。

现实生活中的假设通常不是这样的。事情变得更加模糊了。因此，根据您找到的证据，您的增量可能会上下浮动。在实践中，这意味着不要以表面价值来看待最新的证据。总是把它与你已经知道的东西放在一起。

就像在迟到这个例子中，不增量更新会是这样的：他们今天迟到了，所以我相信“他们总是迟到”。注意你做这件事的频率。

当然，我们做错事也不是十全十美的。如果他们不准时，我会相信“每个人都应该准时。没什么大不了的“，而不是说，他们总是准时。这就是所谓的动机推理。

在我们的示例上下文中，这似乎非常明确。当然，我们会逐步更新。丢弃我们已经获得的所有信息将是愚蠢的。

当我14岁的时候，我听说举重锻炼会阻碍你的成长。我相信“锻炼是邪恶的，每个大个子都吃类固醇”。

当我15岁的时候，我听说你可以只用你的体重来锻炼身体。这不会阻碍增长。我相信“体重锻炼能减掉体重真是太棒了”。

几周后，没有收获，我很沮丧。我相信“这些都不管用。这些都是企业赚钱的骗局。“。我不知道到底是谁在从我的体重训练中赚钱，但话又说回来，我不是一个批判性的思想家。

从那以后，我做了自己的研究。我明白这是一个复杂的问题，它不仅取决于锻炼，不仅取决于你锻炼了多久，还取决于你吃了什么。

我开始逐步更新。我把每一件证据与我到目前为止看到的一切联系起来。不是每个人都用类固醇。力量训练至少对某些人有效。间歇性禁食和跑步对其他人有效。考虑到所有不同的和相互矛盾的证据，我不可能对任何关于锻炼的信念有接近90%的信心。

没有增量更新的一个标志是信念之间的反复无常。你今天看到的证据是完全真实的。

另一种失败模式是排练你的论点。当一个争论不断地浮现在你的脑海中时，那就是没有循序渐进地更新。你拿出你已经用过的同样的证据来增强信心。

一个粗略的例子是，面对新的危险情况时，对自己重复“一切都会好起来的”、“一切都会好起来的”。有时候，有必要让你的神经平静下来。其他时候，就像股市泡沫一样，当证据表明错误的信念不成立时，是你强化了错误的信念。

在一个你钟爱的理论并不正确的世界里，你会期望看到一些不同的东西吗？

在2，4，6游戏中，如果你没有测试任何你认为是错误的东西，你只能找到支持你的假设的证据。你只会对自己的想法更有信心。

反证证据是任何你不希望在你的假设中适用的东西。在第2，4，6场比赛中，这些情况是您期望黑匣子说“不”的情况。因此，对于“3偶数递增”假设，(1，2，3)和(1，-1，2)都可能是不确定的证据。

(1，-1，2)表明您的假设，3即使是正数也可能是正确的，而(1，2，3)表明它确实是错误的。您期望(1，2，3)为“否”，但得到的结果是“是”。8个。

在迟到的例子中，验证“总是迟到”假设的证据是寻找你的同事准时到达的时间。我们往往会忘记这一点，只看他们迟到的时间。这导致了新的问题。

除非你找到不确凿的证据并检验你的假设，否则你的信念就是一座玻璃城堡。玻璃城堡是易碎的。事实上，不证实证据的作用是摧毁城堡，或者在这个过程中让它们变得更坚固。

大脑的自然反应是保护这座玻璃城堡。大脑将不确定的证据视为攻击，而不是感激，我们倾向于将新的证据拒之门外。如果你把不确定的证据当作垃圾来消除，当然你永远不会改变主意。你总是更新以示支持。

你可以在2，4，6游戏中输入一百万个遵循你模式的数字，事情看起来会很好，但你永远不会意识到你的假设是另一个假设的子集(都是正数)-直到有一天你的假设让你失败了。贝叶斯对此无能为力。9个。

因此，一定要寻找不确凿的证据。要做到这一点，您可以查找与您的假设不符的数据，就像我们上面所做的那样。另一种方法是寻找能够更好地解释你已经拥有的数据的假设。用贝叶斯的话说，你是在寻找先前赔率更高的假设。并不是所有的假设都是平等的。有些人能比其他人更好地解释数据。

朱莉娅·加尔夫(Julia Galef)就是一个很好的例子，她追踪了朋友之间的嫉妒。仅仅因为凯伦抱怨，并不意味着她嫉妒。也许任何理智的人都会这么做。

你活过的每一刻都是你可以用来计算下一步的信息。

上一次我们。

.