彼得·诺依曼（Peter M.Neumann），1940–2020年

牛津大学皇后学院数学教授彼得·诺伊曼（Peter Neumann）两周前去世。上周一是他80岁生日。

今天，我们与其他在私下哀悼和在公共场合记忆的人一道，包括这些故事和回忆的作者，这些人都是Peter的39名研究生中的一员。

彼得死于Covid-19，当时他正在养老院接受长期治疗中风的治疗，该中风两年前瘫痪了他的左侧-他写道，他可以从“不晚于2020年末”康复。从我们知道与这种事件密切相关的人的数量（包括我的家人），我们对重大悲剧的统计窗口很小。我们最能为新年做出的一项决议就是带来一项决议，以便Covid 19-20-21的进步就此止步。

对我而言，最能定义Peter的两个词是和acute而敏锐。我从1981年在牛津大学获得Marshall奖学金的研究生身份开始就认识他。牛津大学的每一次“堂课”都与三十九所住宿学院之一或六个私人礼堂相关。我加入默顿学院与我的顾问多米尼克·威尔士（Dominic Welsh）交往，但还有彼得·卡梅隆（Peter Cameron），他的记忆与他息息相关，他在1971年获得彼得（Peter）博士学位后加入了默顿的学院。也许这就是为什么彼得（即诺伊曼）的原因-拼写他的名字eter。

在我的第一学期初期，彼得邀请我参加了奎特（Queter）在皇后学院宽敞的房间举办的每周特别研讨会。它已被称为Kinderseminar，因为它是针对研究生的，他们具有阅读当前研究论文并进行介绍的经验。它通常从上午11点开始，并且在中午之后会有一段灵活的时间，因为牛津大学的午餐通常从学生的12:20或12:30开始，同伴的下午1点开始。

在美国我见过的任何地方都很难复制气氛。至少有一把舒适的大椅子，我记得彼得的学生莎拉·里斯（Sarah Rees）几乎消失了，而其他椅子则围在咖啡桌旁喝茶和（更多时候是）咖啡。一卷McVitie传了出去。除非在最黑暗的日子里，高高的窗户允许充足的光线以关闭灯。闲聊时间结束时，拖着桌子的头是一个便携式黑板。然后开始如何讲授大师班的大师班。

我们已经在此博客上多次提到了研讨会。其中提到的两个回顾了奎特本人在埃法斯特·加洛瓦（ÉvaristeGalois）上的一次演讲，该演讲的最后要点是警告在证据中不慎使用“很容易看到……”之类的危险。奎特解释说，加洛伊斯正好在决斗杀死他的前一天匆忙写作，但我们大多数人没有这个借口。这是奎特关于加洛瓦的保留演讲。

这些帖子中最近发表的是诺曼·比格斯（Norman Biggs），他访问了牛津大学并参加了我第一年的一些研讨会。我在研讨会上的第一个演讲是关于在Biggs的教科书中涵盖的普林斯顿大学定理论文中找到的替代证明。他给我很好的称赞，是说如果他的文字第二版可以使用我的证明。但是奎特-啊，奎特后来把我拉到一边，指出了我在传递它们时的一些缺陷，包括身体的位置以及在板上组织图表和代数的过程。当然，令人鼓舞。

我的Mertonian和国际象棋大师Dugald Macpherson也是一位常客。我们俩都不是进入那个房间的最杰出的国际象棋棋手，因为大师傅科林·麦克纳布（Colin McNab）在我毕业后不久就获得了etereter的博士学位。来访的肯·约翰逊（Ken Johnson）在牙买加打一流板球的故事给我留下了深刻的印象。三十年后，当我从普林斯顿大学南部校园停车场的汽车中出来，登上一辆前往参加2012年艾伦·图灵百年纪念活动的Jitney时，有约翰逊（Johnson），他现在是宾州州立大学的教授。我对其他学生特别有记忆，包括穆罕默德·奥杜（Muhammad Audu），雅辛塔·科温顿（Jacinta Covington）和蒂姆·彭蒂拉（Tim Penttila）。

1983年10月25日，星期二，一个古怪的回忆出现了，在广播中找到所有人，并带上了美国入侵格林纳达的简报，该简报是从当地黎明开始的。经过一些反对帝国主义的尖锐反对之后，他们的确进入了数学领域，但是我的脑海仍然留在格林纳达，因为我脑海里写着钢鼓旋律和那首还未完成的关于这件事的歌曲的第一节。

因为他在2008年来自伊丽莎白女王府的OBE说彼得不是彼得，所以我将回到前者。它被引用为数学教育服务。他不仅赢得了其他奖项，而且还有一个以他命名的奖项：英国数学史学会的诺伊曼奖。彼得曾经担任过主席，还领导了英国数学协会-英国徽标的名称用小写字母拼写。

从各种经验中，我可以断定彼得采取了全人教育的方式。他跟随他以前的学生的生活，我听到了在英国和法国发生的社交场合的故事。他还为学生撰写了牛津数学学院的TeX和LaTeX指南。

1984年5月，研究所在牛津以北约55英里的考文垂附近的沃里克大学组织了一次数学日郊游。彼得组织了大约十二次旅行-不管是所有人都是来自牛津，而且无论我们有班车还是单独的车，我都不记得了。

我确实记得他不是简单地带我们进出研讨会。他计划在奥克森-瓦尔克斯（Oxon-Warks）边界沿道路的Rollright Stones上野餐。我以前从未见过凯尔特人的石圈。他讲述了它的历史故事。我还相信，会议结束后，我们驱车驶入考文垂，短暂停留在大教堂周围，看看第二次世界大战造成的破坏，但我有可能将牛津国际象棋队的比赛与之混为一谈。考文垂。

彼得在团体理论中具有诺伊曼谱系，因为这是他母亲和父亲的特长。他在有关约旦-霍尔德定理历史的论文中指导了来自默顿的另一个朋友朱莉娅·汤普森。但是，我将讨论小组理论作为背景的贡献，其中我可以将计算复杂性的观点放在前台。

我们在2014年5月发布的文章“ STOC 1500”具有半认真的意图，将几何（非）可构造性的著名经典问题与现代复杂性理论相结合。它由国际象棋大师和数学家卢卡·帕乔利（Luca Pacioli）作了幻想的主题演讲，并介绍了“？”问题：仅使用Euclid的标尺和指南针，可以将一个三等分的角度，两倍的立方体或（超出的）正方形的一个圆？就像我们很费力地说“”不代表“非多项式”一样，“”这个名字并不代表“不可构造”，而是可以通过胶结来构造，这意味着在可旋转标尺上使用固定标记。当然，现在我们知道，一个事实通常归因于伽罗瓦理论，但是，正如彼得在他的论文中指出的那样，可以从关于场扩展的更简单考虑中得到证明。

“古代复杂度”和计算复杂度在实例和问题之间都有关键的区别。将角度三等分很容易。如果是一个可构造的角度，则可以将角度三等分-但是该方法是特定于该实例的，没有一个仅给出的算法会有效地发现如何将其三等分。有些算法可以在多个角度上正常工作，但不能在所有角度上正常工作。

与计算复杂度最不同的是，存在无法解决的单个实例，例如。这不是基于Euclid的算法花费太长时间的情况：没有算法可以构造角度，周期。这类似于在Kolmogorov复杂度中单个字符串不可压缩的方式，但是后者不依赖于参考通用压缩方案。

另一个区别是本质上只有一个实例的问题，例如将立方体加倍并对圆进行平方。可以施加代数坐标来表示它们的不同实例，但这与标记给定标尺的标记所允许的，不同于根据给定实例的特征定义坐标的方法不同。彼得的论文很好地说明了这些问题/实例的区别。

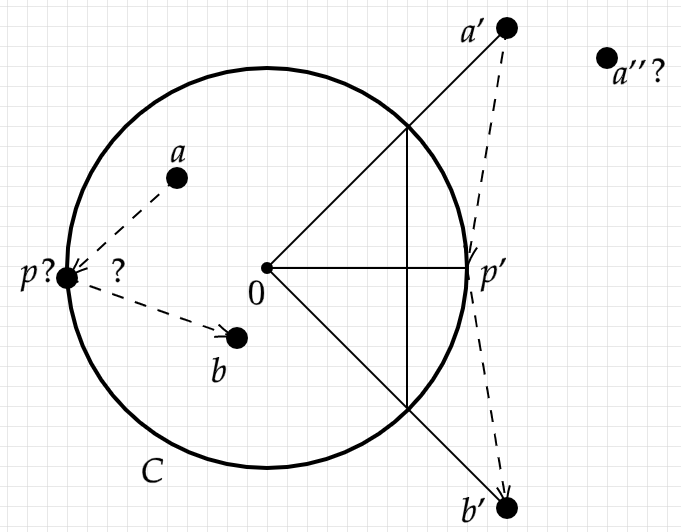
彼得的论文中解决的问题是托勒密（Ptolemy）在150年提出的。给定一个圆和点，并且在内部或外部都构造一个点，这样，从处开始的光将反射并进入。当这些点都在里面时，可以想象这是从圆形边缘射出一个完美的台球击中。

有两种算法可以正确求解无数个实例集，即与圆心等距的点。一个构造在和之间的线段的中点，将射线从投射到，并找到射线相交的位置。另一个（如上图所示）首先找到到的光线的交点，将连接它们的线段一分为二，然后使用该线段向外投射到。后一种算法还适用于分别与到和的光线共线的点，而前一种算法对于从穿过且与平行的线中选取的对是正确的。如果不可用，则可以组合使用这些方法以处理原始等距情况。

在1020年左右，哈桑·伊本·海瑟姆（Hasan Ibn al-Haytham）提出了一种在所有情况下均有效的几何算法，使用圆锥形截面的方式等效于神经突切，并由圣何塞州的罗杰·阿尔珀林（Roger Alperin）进一步描述了这一千年。直到1965年杰克·艾尔金（Jack Elkin）发表论文时，这个问题显然才被发现是外部的。

在考虑了上述论文中可解决的情况之后，Elkin最后给出了一个非案例，类似于三等分问题。他的例子确实显示了一般的代数成分。彼得在1998年的论文中显然没有意识到Elkin的所作所为，是对所有可解决的案例进行了刻画，并表明它们构成了一组零度量。因此，他给出了一种严格的感觉，即几乎所有反射问题都无法解决。在彼得的论文中，关于场扩展和不可约性的代数和引理特别漂亮。

我们对彼得的妻子西尔维亚，他的家人以及所有认识他的人表示哀悼。伦敦数学协会的这份通知最后包括邀请函，以邀请女王学院收集的藏品。

在撰写本文的同时发现Alperin的等效性，使我重新提出“ STOC 1500”文章中的这个问题：是否存在一个唯一的问题，即-完全减少-减少？