矩阵
2022-2-26 7:23
NumPy中的矩阵乘法速度相当快,无需优化。然而,如果每秒钟都很重要,就有可能显著提高性能(即使没有GPU)。
下面是一些小技巧的集合,可以帮助进行大型(~4000x4000)矩阵乘法。我用它们将深层神经网络的推理时间从24秒缩短到不到一秒。事实上,在一个例子中,我在CPU上优化的代码比使用GPU的Tensorflo......
2021-7-31 22:23
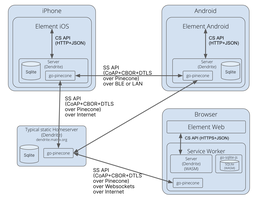
这个项目是白板(类似于oneNote),它使用Matrix作为其后端。您的所有图纸都存储在矩阵服务器上的矩阵房间中,任何受邀者均可访问。白板事件的规范仍可能发生变化。除了在 Alpha 测试期间,不建议将其用于任何其他用途!建议始终创建单独的房间,仅用于测试此应用程序。所以当协议改变时,它们可以被留下并被新的替换!很......
2021-5-8 22:52
自2019年底以来,我们花了很多时间思考和探索不同的技术,同时为P2P矩阵构建各种演示。我们对P2P矩阵的使命是将矩阵延伸到今天之间的混合动力和纯粹的P2P网络之间的混合动力和纯P2P网络 - 如果他们想要的数据(通过将其存储在P2P矩阵中,则为用户提供全部自主权和隐私通过将他们的服务器嵌入到他们的矩阵客户端中),同......
2021-3-11 0:57
等级学校数学学生可能熟悉教师劝告他们不要只是猜到问题的答案。但是,一个新的证据确定了,实际上,正确的猜测有时是解决线性方程系统的最佳方法,是数学的基岩计算之一。
因此,证据建立了能够超越先前对这些类型问题的速度难以解决的难度限制的第一种方法。
“这是计算中最基本的问题之一,”滑铁卢大学的马克·格斯布莱克说。 “现......
2021-2-21 22:4
是的,就在这里!在对alpha,beta和RC进行了几次迭代之后,科迪团队很高兴地宣布Kodi 19.0" Matrix"刚刚在所有受支持的平台上正式发布。敢于服用红色药丸,然后找出兔子洞有多深?
自从18.x" Leia"的第一个版本发布以来,在1,500多个请求中约有5,000......
2021-1-1 17:19
稀疏矩阵是大多数元素的值为0的矩阵。如果非零元素(NNZ)的数量与大小的比值小于0.5,则该矩阵是稀疏的。对于仅包含NNZ元素的矩阵,将使用术语稀疏;对于包含所有元素的矩阵,将使用术语稠密。
存储有关所有0个元素的信息效率很低,因此我们假设未指定的元素为0.使用这种方案,稀疏矩阵可以比其对应的密集矩阵表示执行更快......
2020-11-21 23:23
在深度学习(DL)时代,越来越多的人遇到并使用(已知或不知道)随机矩阵。在大多数情况下,这种使用仅限于网络权重的初始化,这可以通过您喜欢的DL框架中的单行代码来完成。但是,随机矩阵具有丰富的数学理论,在物理学,网络理论,机器学习,金融等领域具有广泛的应用。这种引人入胜的应用范围还意味着每个领域都经常开发其专用术语来描......
2020-11-4 14:59
在我们之前的博客文章中,我们介绍了使用硅光子学来执行大规模线性算术运算的想法,其速度和效率比使用数字电子技术更快、更高效。您可能还记得,我们的系统使用许多称为马赫-曾德尔干涉仪(MZI)[1]的相同器件来实现基本的线性运算,即2x2矩阵乘法,由此可以构建更大的矩阵乘法。在这篇博客文章中,我们的目标是更详细地描述MZI......
2020-8-24 22:13
主成分分析(PCA)是获取高维数据的一系列技术之一,它使用变量之间的依赖关系将其表示为更易处理、更低维的形式,而不会丢失太多信息。它已被广泛用于数据压缩和去噪。然而,它的整个数学过程有时对用户来说是模棱两可的。
在这篇文章中,我想从数学上讨论PCA的整个过程,包括PCA的投影和重建,并提供了大部分的推导和证明。在文章......
2020-8-6 19:42
主成分分析(PCA)是获取高维数据的一系列技术之一,它使用变量之间的依赖关系将其表示为更易处理、更低维的形式,而不会丢失太多信息。它已被广泛用于数据压缩和去噪。然而,它的整个数学过程有时对用户来说是模棱两可的。
在这篇文章中,我想从数学上讨论PCA的整个过程,包括PCA的投影和重建,并提供了大部分的推导和证明。在文章......
2020-7-22 13:43
主成分分析(PCA)是获取高维数据的一系列技术之一,它使用变量之间的依赖关系将其表示为更易处理、更低维的形式,而不会丢失太多信息。它已被广泛用于数据压缩和去噪。然而,它的整个数学过程有时对用户来说是模棱两可的。
在这篇文章中,我想从数学上讨论PCA的整个过程,包括PCA的投影和重建,并提供了大部分的推导和证明。在文章......
2020-6-21 22:19
$\Beginggroup$我目前正在努力自学线性代数。我注意到很多术语(如特征向量、特征多项式、行列式等等)的定义都需要一个方阵,而不是任何实数矩阵。例如,Wolfram在其特征多项式的定义中具有以下内容:
特征多项式是特征方程$\det(A-i\lambda)=0$的左侧多项式,其中$A$是方阵。
为什么矩阵必须......
2020-6-17 23:41
当表示理论在19世纪末出现时,许多数学家质疑它的价值。1897年,英国数学家威廉·伯恩赛德(William Burnside)写道,他怀疑这种非正统的观点会产生任何新的结果。
悉尼大学教授乔治威廉姆森(Geordie Williamson)在2015年的一次演讲中表示:“基本上(伯恩赛德当时的意思)是,代表权理论毫无......
2020-6-10 13:18
当表示理论在19世纪末出现时,许多数学家质疑它的价值。1897年,英国数学家威廉·伯恩赛德(William Burnside)写道,他怀疑这种非正统的观点会产生任何新的结果。
悉尼大学的乔治威廉姆森(Geordie Williamson)在2015年的一次演讲中说:“基本上(伯恩赛德的)意思是,表象理论是没用的。”
......