美国手机数据发现新冠肺炎距离水平低的热点地区
社会疏远,一种旨在减少新冠肺炎传播的非药物策略,可能是因为个人自愿与他人保持距离,以避免感染这种疾病。或者,它也可能是由于地方当局施加的司法限制而出现的。我们对49个州运行作为县级外生人口变量和司法固定效应函数的简化形式的社会距离模型,以评估人口和司法影响在解释社会距离行为中的相对贡献。为了考虑到传染性疾病的可能的空间方面,我们还对与周围县的人口变量相关的溢出进行了建模,并考虑到依赖于周围县的干扰。我们每周运行我们的模型,并检查自美国新冠肺炎大流行开始以来估计系数随时间的演变。这些估计系数表达了那些能够并选择呆在家里以避免疾病的人所揭示的偏好。使用手机跟踪数据测量的居家行为显示出相当大的横截面差异,从2020年1月底到2020年3月底增加了9倍以上,然后到2020年6月中旬下降了约50%。我们的估计结果表明,与司法固定效应的预测相比,人口外生变量对这种差异的解释要多得多。此外,人口外生变量和司法固定效应的解释显示,在样本期间,相关关系不断演变,最初部分抵消,最终相互强化。此外,从人口统计外生变量预测的社会距离表现出显著的空间自回归相关性,表明社会距离行为具有聚集性。居家行为的差异增加,加上高度的空间依赖,可能导致社会距离的相对强烈的热点和冷点,这对疾病的传播和缓解具有重要意义。
像新冠肺炎这样的传染病的传播取决于它的基本繁殖数R0,即与感染者接触直接产生的预期病例数量。社交距离是一种非药物策略,可以通过限制与感染者的接触来降低R0。如果个人喜欢呆在家里以避免感染,并且有能力呆在家里,那么社会距离可能会自然产生。或者,它可以由政府法令引起,作为一种非药物干预,通过限制司法管辖区内的个人活动来遏制疾病的传播。在这篇文章中,我们使用美国手机跟踪数据来检验这些因素是如何解释社交距离的。我们还检查了不同司法管辖区的个体行为是否有所不同,或者是否表现出其他空间模式。
建立社交距离模型需要面对两个问题。第一,社会疏远取决于新冠肺炎的盛行,新冠肺炎的传播取决于社会疏远。因此,社会距离和新冠肺炎的传播是同时决定的,这使得对它们各自影响的估计变得复杂[1,第151页]。其次,各个司法管辖区追踪疾病的不同方式可能会引入测量误差问题,从而使识别工作进一步复杂化[1,第134页]。就获得测试的过程可能取决于人口密度(农村与城市)、年龄、教育、种族和收入等人口统计变量而言,这可能导致与模型中的变量相关的测量误差。例如,免下车测试已经变得流行起来,但这可能会对没有车的贫困居民产生不利影响。与模型中变量相关的测量误差称为微分测量误差,这会导致估计的偏差[2]。
为了避免同步和测量误差的问题,我们将重点放在社交距离的简化形式建模上,通过使用手机跟踪数据每周呆在家里的个人百分比日志的变化来衡量社交距离。简化形式涉及因变量作为外部人口变量(人口密度、年龄、教育、种族和收入)以及49个州的司法固定影响(由于数据覆盖而不包括夏威夷)的函数的回归。由于传染性疾病的空间性质,我们还对与周围县的人口变量相关的溢出效应进行了建模,并考虑到县级的空间依赖性干扰。这也反映了自然灾害可能的空间方面[3,4]。我们对每周的数据进行单独的简化形式回归,并检查自美国新冠肺炎大流行开始以来估计系数随时间的演变。这些估计系数
人口统计数据收集自美国人口普查提供的美国社区调查(ACS)数据。我们使用2018年结束的5年预估,因为这是最新的ACS数据,其中包括美国每个县的覆盖范围。我们将一个县的人口规模视为美国2019年7月1日人口普查估计的人口规模。为了将人口水平转换为人口密度,我们从2019年发布的美国人口普查地名词典数据中获得县土地面积。
表1报告了本研究中使用的外生变量的汇总统计数据。人口密度(POP)是最不对称的变量,每平方英里(亚肯色州育空-小柳克)最少0.04人,每平方英里(纽约州)最多71872.6人。在中位数的县,29.3%的家庭至少有一个18岁以下的孩子(Child)。在中位数的县,87%的人口没有获得学士学位或更高学位(HS),89.9%的人口是白人(White)。中等县的家庭收入中位数为49871.8美元。
我们使用来自SafeGraph的GPS数据推断出县级的个人呆在家里的比率。该公司通过手机的GPS ping收集个人的匿名位置数据。为了应对大流行,SafeGraph向研究人员发布了他们的聚合和匿名数据,并开始发布额外的数据,包括社会距离度量数据集。此数据集覆盖了美国所有50个州以及华盛顿特区。我们发现夏威夷的县覆盖范围不完整,因此将其排除在我们的分析之外。社交距离度量数据记录,汇总到人口普查区块组(CBG)级别、指定日期CBG中的活动设备数以及在该天从未离开用户推断的家庭位置的设备计数。我们将这些CBG级别的数字汇总到县级别,然后通过将家里的设备数量完全除以活动设备的总数来定义我们的社交距离代理。然后,在给定的一周内,设备呆在家里的平均比率就是该县的社会距离水平。
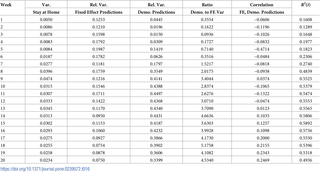
表2展示了从2020年1月的第三周开始,在我们样本中的21周数据中,这一社交距离度量的演变情况。在特朗普总统于2020年3月14日(第7周)发表国家紧急状态宣言之前,人们社交疏远的比例中值约为25%。声明发布后,在第8周到第12周呆在家里的人数急剧增加。4月中旬,当各个州放松了对呆在家里的限制时,这一数字开始下降,但相对于紧急状态前的水平仍保持在较高水平。社交距离范围的变化在几周内表现出类似的模式。
总统的紧急状态声明并不是政府对大流行的唯一回应。各国通过发布非药物干预措施(NPI)来应对医疗危机,例如强制关闭某些企业。响应因州而异,并且在我们的样本期内在不同的时间点实施。此外,这些法律上的NPI具有不同的事实上的实施/执行。正如[20]文件所述,在暴发期间的不同时间实施了各种各样的实际政策。这种异质性阻碍了对特定测量的直接建模。为了解决这些问题,我们包括了状态固定效应和其他控制变量。潜在限制的效力将隐含地表现为每周不断变化的参数估计。
我们还从“纽约时报”获得了县级疾病数据,并在表3中报告了新疾病计数的汇总统计数据,以供说明。疾病跟踪的高度分散性质导致了美国疾病病例数据中的重大问题。由于检测资格(个人是否可以接受检测)、检测通道(县是否有检测包可用)、检测规则(例如,是否需要对死者进行检测)和报告规则(例如,非居民的结果分类)方面的差异,县一级存在着很大的异质性。如表3所示,在国家紧急状态宣布的那一周,只有不到5%的县报告了新病例。这不是因为此时病例很少,而是因为在大流行的头几个月里检测的可用性受到限制[21,22]。这些数据中存在的各种测量误差来源或选择机制促使我们使用避免案例数据的方法。我们将在下一节中讨论这一点的统计理由。
如前所述,病毒的传染性取决于社会距离,而社会距离可能取决于病毒的传染性和毒性。理想情况下,可以将它们建模为联立方程
然而,(2)中的结构方程的识别和估计有时被证明是具有挑战性的。获得识别的最常见方法需要一个变量(工具),该变量影响一个内生变量,而不影响另一个。不幸的是,这种异质性条件无法通过经验进行测试,并成为分析中的一个潜在弱点。此外,跨司法管辖区报告新冠肺炎检测、住院和死亡的不统一性质引发了有关病毒测量误差的问题。在联立方程系统中,一个方程(病毒)的测量误差会影响另一个方程(社会距离)。为了避免这种情况,我们求助于建模无限制简化形式[23,p.528],如(3)所示。在无约束的简化形式下,当使用X中的所有外生变量时,每个因变量都可以被一致地估计。所得到的参数估计Πt在(4)中显示了特定外生变量对因变量的影响。(3)(4)。
因为外生变量X不会随着时间的推移而改变,所以每个横截面估计值可以产生不同的Πt估计值。这样,个体对避免病毒的愿望的选择可以表达对疾病存在的进化反应。呆在家里显示出对安全的偏好(取决于呆在家里的能力)。我们感兴趣的是疾病发生时行为的变化,为了做到这一点,我们对时间t和时间0的简化形式的方程进行了差分,如(5)所示。(5)。
注意,对于无约束的约化形式,我们可以逐个方程地估计这个方程。在这种情况下,由于重点在于社会距离作为外生变量的函数,我们可以转到更简单的单方程模型,这是下一节要讨论的主题。
综上所述,社会距离和疾病是同时确定的,将内生变量之一视为典型的右侧变量的简单单方程估计可能会导致不一致的估计。虽然可以尝试使用结构形式同时对这些变量建模,但识别这些系统可能是具有挑战性的。此外,疾病数据有许多不统一的报告问题,可能会对估计产生不利影响。为了避免这种情况,我们求助于不受限制的简化形式建模。由于外生变量在疾病期间保持不变,疾病流行的影响显示在不断演变的参数估计中。通过对时间0和时间t的简化形式求差,我们看到个体行为的变化是外生变量的函数。
在这一节中,我们将描述基于上一节中简化形式的解释在估计中使用的实际单方程模型。我们首先将y(T)定义为每周t,h(T)待在家里的人口百分比的对数,如(6)所示。与上一节不同,我们切换到以t为索引的参数表示法,因为这允许对模型中的各种组件使用下标和幂。模型中参数、干扰和因变量的t指数化表明了一系列的横截面回归,其中参数值随时间的变化反映了个体对呆在家里的安全的显露偏好。因为我们关注的是y(T)随时间的相对变化,所以(7)中的因变量Δ(T)等于y(T)−y(0)。使用变化可以帮助减少对周期0和t有类似影响的省略变量。由于我们的差异期相对较短(最多20周),许多来自省略变量的影响可能会减少。(6)(7)。
我们选择变量来代表人口密度、年龄、教育程度、种族和收入的基本人口特征。为了便于解释,我们从每个主要类别中只选择了一个变量。具体地说,解释变量包括人口密度的对数(POP)、有18岁以下儿童的家庭百分比的对数(CHILD)、没有大学学历的工人的百分比的对数(HS)、人口中白人的百分比的对数。
.